QURA: a quantum algorithm for reversing unknown physical transformations
Can we reverse the physical evolution using quantum computing? 🤔 The answer lies in our developed quantum algorithm known as QURA, reversing any unitary operation without prior knowledge of its characteristics.
Quantum computing leverages the peculiarities of quantum mechanics to potentially outperform classical computing in astonishing ways. Among its marvels is the concept of quantum teleportation, a process that allows for the transfer of quantum information across space without the need to know the specific details of the quantum state being transmitted. Our team has studied this domain to explore an interesting question: Can we reverse the evolution of a quantum system even if we lack knowledge about its nature?
The reversibility of quantum unitaries distinguishes quantum computing from its classical counterpart with irreversible operations. The evolution of systems under a unitary operator can be represented by a solution of the Schrödinger's equation, $U=e^{-iHt}$, with the unitary inverse being $U^{-1}=e^{iHt}$. Achieving the unitary inversion plays a pivotal role in quantum computing and is a ground component of many quantum algorithms. Nevertheless, the challenge arises when these unitary processes are hidden within a ‘black box’—when their Hamiltonian, $H$, is unknown. How then can we achieve their inversion? This conundrum, both fascinating and formidable, remained unsolved until the pioneering work of Murao's group1, which provided the first deterministic and exact method for inverting 2-dimensional unitary operators. However, the solution for arbitrary dimension remained unsolved.
Our group has achieved a breakthrough by creating a universal algorithm capable of deterministically and exactly reversing any unknown unitary operation, $U$, regardless of its dimension2. The algorithm's idea lies in its "intrinsic encoder" and "shifted decoder" subcircuits, which together form what we call the "duality-based amplitude amplifier". In this algorithm, the intrinsic encoder first achieves $U^{-1}$ with a small amplitude through a linear combination of given U. Then, the amplifier gradually increases this component's amplitude to 1, eventually achieving $U^{-1}$.
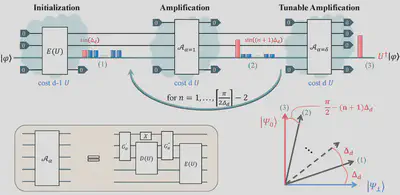
QURA can be well-explained through a traditional manner, yet its conception was inspired in a more avant-garde idea: parameterized quantum circuits (PQC). Our team used PQC to search circuit structures for reversing unknown 2-dimensional unitary operators3. Further analysis and generalization of this result then contributes to the derivation of QURA.

Our finding presents the first deterministic and exact method for inverting unknown quantum time evolutions across any dimension. The computational complexity of our algorithm scales linearly with the dimension, denoted as $\mathcal{O}(d)$, showcasing a quantum advantage that quadratically surpasses classical approaches. It requires a mere $\mathcal{O} (d^2)$ queries of the unknown $U$, which may suggest a near-optimality of our method. This innovation not only serves as a ground component in the construction of a key oracle for unitary inversion but also enriches the toolkit available within quantum algorithm frameworks such as quantum singular value transformation.
Satoshi Yoshida, Akihito Soeda, and Mio Murao. Reversing Unknown Qubit-Unitary Operation, Deterministically and Exactly. ↩︎
Yu-ao Chen, Yin Mo, Yingjian Liu, Lei Zhang, and Xin Wang. Quantum Advantage in Reversing Unknown Unitary Evolutions. ↩︎
Yin Mo, Lei Zhang, Yu-ao Chen, Yingjian Liu, Tengxiang Lin, and Xin Wang. Parameterized quantum comb and simpler circuits for reversing unknown qubit-unitary operations. ↩︎