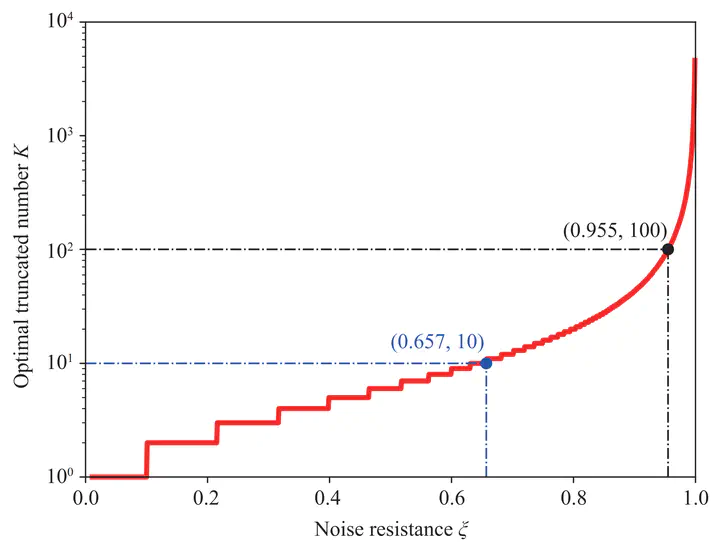
 The degree of truncated Neumann series as a function of the noise resistance.
The degree of truncated Neumann series as a function of the noise resistance.Abstract
Quantum gates and measurements on quantum hardware are inevitably subject to hardware imperfections that lead to quantum errors. Mitigating such unavoidable errors is crucial to explore the power of quantum hardware better. In this paper, we propose a unified framework that can mitigate quantum gate and measurement errors in computing quantum expectation values utilizing the truncated Neumann series. The essential idea is to cancel the effect of quantum error by approximating its inverse via linearly combining quantum errors of different orders produced by sequential applications of the quantum devices with carefully chosen coefficients. Remarkably, the estimation error decays exponentially in the truncated order, and the incurred error mitigation overhead is independent of the system size, as long as the noise resistance of the quantum device is moderate. We numerically test this framework for different quantum errors and find that the computation accuracy is substantially improved. Our framework possesses several vital advantages: it mitigates quantum gate and measurement errors in a unified manner, it neither assumes any error structure nor requires the tomography procedure to completely characterize the quantum errors, and most importantly, it is scalable. These advantages empower our quantum error mitigation framework to be efficient and practical and extend the ability of near-term quantum devices to deliver quantum applications.