Illustration of the capabilities of quantum phase processing.Abstract
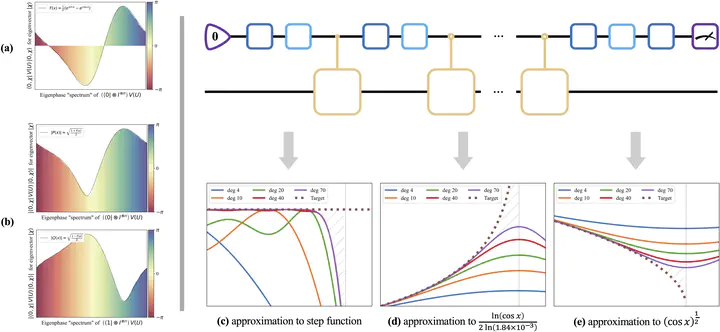
Quantum computing can provide speedups in solving many problems as the evolution of a quantum system is described by a unitary operator in an exponentially large Hilbert space. Such unitary operators change the phase of their eigenstates and make quantum algorithms fundamentally different from their classical counterparts. Based on this unique principle of quantum computing, we develop an algorithmic toolbox, quantum phase processing, that can directly apply arbitrary trigonometric transformations to eigenphases of a unitary operator. The quantum phase processing circuit is constructed simply, consisting of single-qubit rotations and controlled unitaries, typically using only one ancilla qubit. Besides the capability of phase transformation, quantum phase processing in particular can extract the eigeninformation of quantum systems by simply measuring the ancilla qubit, making it naturally compatible with indirect measurement. Quantum phase processing complements another powerful framework known as quantum singular value transformation and leads to more intuitive and efficient quantum algorithms for solving problems that are particularly phase related. As a notable application, we propose a quantum phase estimation algorithm without quantum Fourier transform, which requires the fewest ancilla qubits and matches the best performance so far. We further exploit the power of our method by investigating a plethora of applications in Hamiltonian simulation, entanglement spectroscopy, and quantum entropy estimation, demonstrating improvements or optimality for almost all cases.'
Lei Zhang
PhD Student
I obtained my BMath in AMath, CO & joint PMath from the University of Waterloo. My research interests include quantum information theory and quantum machine learning.
Xin Wang
Associate Professor
Prof. Xin Wang founded the QuAIR lab at HKUST(Guangzhou) in June 2023. His research primarily focuses on better understanding the limits of information processing with quantum systems and the power of quantum artificial intelligence. Prior to establishing the QuAIR lab, Prof. Wang was a Staff Researcher at the Institute for Quantum Computing at Baidu Research, where he concentrated on quantum computing research and the development of the Baidu Quantum Platform. Notably, he spearheaded the development of Paddle Quantum, a Python library designed for quantum machine learning. From 2018 to 2019, Prof. Wang held the position of Hartree Postdoctoral Fellow at the Joint Center for Quantum Information and Computer Science (QuICS) at the University of Maryland, College Park. He earned his doctorate in quantum information from the University of Technology Sydney in 2018, under the guidance of Prof. Runyao Duan and Prof. Andreas Winter. In 2014, Prof. Wang obtained his B.S. in mathematics (with Wu Yuzhang Honor) from Sichuan University.