Efficient information recovery from Pauli noise via classical shadow

Abstract

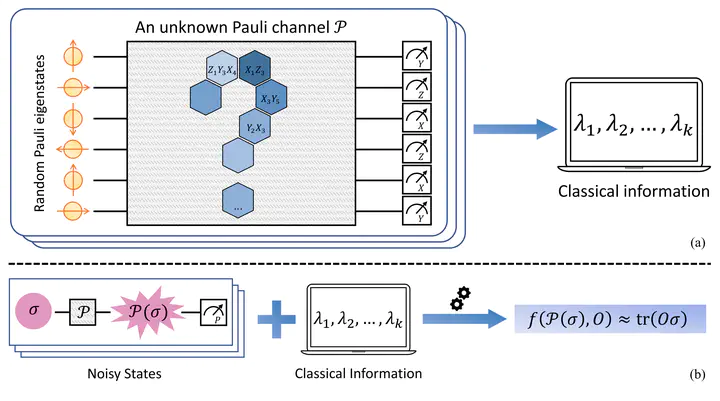
The rapid advancement of quantum computing has led to an extensive demand for effective techniques to extract classical information from quantum systems, particularly in fields like quantum machine learning and quantum chemistry. However, quantum systems are inherently susceptible to noises, which adversely corrupt the information encoded in quantum systems. In this work, we introduce an efficient algorithm that can recover information from quantum states under Pauli noise. The core idea is to learn the necessary information of the unknown Pauli channel by post-processing the classical shadows of the channel. For a local and bounded-degree observable, only partial knowledge of the channel is required rather than its complete classical description to recover the ideal information, resulting in a polynomial-time algorithm. This contrasts with conventional methods such as probabilistic error cancellation, which requires the full information of the channel and exhibits exponential scaling with the number of qubits. We also prove that this scalable method is optimal on the sample complexity and generalise the algorithm to the weight contracting channel. Furthermore, we demonstrate the validity of the algorithm on the 1D anisotropic Heisenberg-type model via numerical simulations. As a notable application, our method can be severed as a sample-efficient error mitigation scheme for Clifford circuits.

Chenghong Zhu

PhD Student (2023)

I obtained my BS and MS degrees in computer science from the University of Melbourne. My research interests include distributed quantum computing, quantum entanglement and quantum machine learning.

Xin Wang

Associate Professor

Prof. Xin Wang founded the QuAIR lab at HKUST(Guangzhou) in June 2023. His research primarily focuses on better understanding the limits of information processing with quantum systems and the power of quantum artificial intelligence. Prior to establishing the QuAIR lab, Prof. Wang was a Staff Researcher at the Institute for Quantum Computing at Baidu Research, where he concentrated on quantum computing research and the development of the Baidu Quantum Platform. Notably, he spearheaded the development of Paddle Quantum, a Python library designed for quantum machine learning. From 2018 to 2019, Prof. Wang held the position of Hartree Postdoctoral Fellow at the Joint Center for Quantum Information and Computer Science (QuICS) at the University of Maryland, College Park. He earned his doctorate in quantum information from the University of Technology Sydney in 2018, under the guidance of Prof. Runyao Duan and Prof. Andreas Winter. In 2014, Prof. Wang obtained his B.S. in mathematics (with Wu Yuzhang Honor) from Sichuan University.