Abstract
Quantum Markov chains generalize classical Markov chains for random variables to the quantum realm and exhibit unique inherent properties, making them an important feature in quantum information theory. In this work, we propose the concept of virtual quantum Markov chains (VQMCs), focusing on scenarios where subsystems retain classical information about global systems from measurement statistics. As a generalization of quantum Markov chains, VQMCs characterize states where arbitrary global shadow information can be recovered from subsystems through local quantum operations and measurements. We present an algebraic characterization for virtual quantum Markov chains and show that the virtual quantum recovery is fully determined by the block matrices of a quantum state on its subsystems. Notably, we find a distinction between two classes of tripartite entanglement by showing that the W state is a VQMC while the GHZ state is not. Furthermore, we establish semidefinite programs to determine the optimal sampling overhead and the robustness of virtual quantum Markov chains. We demonstrate the optimal sampling overhead is additive, indicating no free lunch to further reduce the sampling cost of recovery from parallel calls of the VQMC states. Our findings elucidate distinctions between quantum Markov chains and virtual quantum Markov chains, extending our understanding of quantum recovery to scenarios prioritizing classical information from measurement statistics.
Publication
arXiv:2312.02031

Research Associate
I obtained my BS in Mathematics and Applied Mathematics from University of Science and Technology of China. I obtained my PhD degree in Applied Mathematics from University of Chinese Academy of Sciences under the supervision of Prof. Xiao-Shan Gao. My research interests include quantum computing, symbolic computation and cryptanalysis.

PhD Student
I obtained my BS in Applied Mathematics from China Agricultural University under the supervision of Prof. Zhencai Shen. I obtained my MS degree in Cyberspace Security from University of Chinese Academy of Sciences under the supervision of Prof. Zhenyu Huang. My research interests include quantum information theory and quantum computation.

Research Assistant
I obtained my BS in Electronic Information Science and Technology from Chongqing University. I obtained my MS degree in Electrical Engineering from University of Southern California. My research interests include quantum information theory and quantum computation.

PhD Student
I obtained my BS and MS degrees in physics from the University of Melbourne. My research interests include distributed quantum computing, quantum entanglement and quantum machine learning.

Associate Professor
Prof. Xin Wang founded the QuAIR lab at HKUST(Guangzhou) in June 2023. His research primarily focuses on better understanding the limits of information processing with quantum systems and the power of quantum artificial intelligence. Prior to establishing the QuAIR lab, Prof. Wang was a Staff Researcher at the Institute for Quantum Computing at Baidu Research, where he concentrated on quantum computing research and the development of the Baidu Quantum Platform. Notably, he spearheaded the development of Paddle Quantum, a Python library designed for quantum machine learning. From 2018 to 2019, Prof. Wang held the position of Hartree Postdoctoral Fellow at the Joint Center for Quantum Information and Computer Science (QuICS) at the University of Maryland, College Park. He earned his doctorate in quantum information from the University of Technology Sydney in 2018, under the guidance of Prof. Runyao Duan and Prof. Andreas Winter. In 2014, Prof. Wang obtained his B.S. in mathematics (with Wu Yuzhang Honor) from Sichuan University.
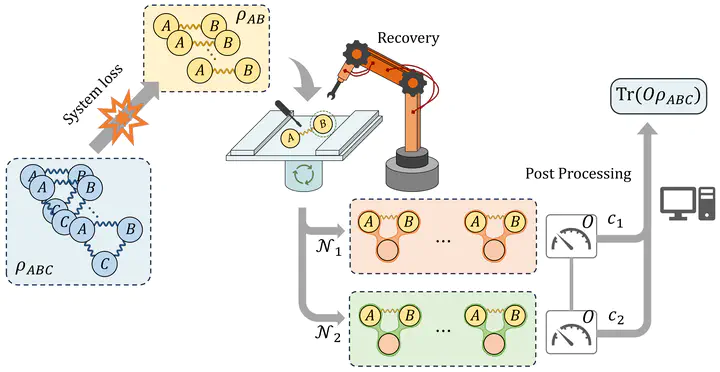 The framework of virtual quantum recovery.
The framework of virtual quantum recovery.