Abstract
Abstract Quantum entanglement is a crucial resource in quantum information processing. However, quantifying the entanglement required to prepare quantum states and implement quantum processes remains challenging. This paper proposes computable and faithful lower bounds for the entanglement cost of general quantum states and quantum channels. We introduce the concept of logarithmic k-negativity, a generalization of logarithmic negativity, to establish a general lower bound for the entanglement cost of quantum states under quantum operations that completely preserve the positivity of partial transpose (PPT). This bound is efficiently computable via semidefinite programming and is non-zero for any entangled state that is not PPT, making it faithful in the entanglement theory with non-positive partial transpose. Furthermore, we delve into specific and general examples to demonstrate the advantages of our proposed bounds compared with previously known computable ones. Notably, we affirm the irreversibility of asymptotic entanglement manipulation under PPT operations for full-rank entangled states and the irreversibility of channel manipulation for amplitude damping channels. We also establish the best-known lower bound for the entanglement cost of arbitrary dimensional isotropic states. These findings push the boundaries of understanding the structure of entanglement and the fundamental limits of entanglement manipulation.
Publication
arXiv:2311.10649

Associate Professor
Prof. Xin Wang founded the QuAIR lab at HKUST(Guangzhou) in June 2023. His research primarily focuses on better understanding the limits of information processing with quantum systems and the power of quantum artificial intelligence. Prior to establishing the QuAIR lab, Prof. Wang was a Staff Researcher at the Institute for Quantum Computing at Baidu Research, where he concentrated on quantum computing research and the development of the Baidu Quantum Platform. Notably, he spearheaded the development of Paddle Quantum, a Python library designed for quantum machine learning. From 2018 to 2019, Prof. Wang held the position of Hartree Postdoctoral Fellow at the Joint Center for Quantum Information and Computer Science (QuICS) at the University of Maryland, College Park. He earned his doctorate in quantum information from the University of Technology Sydney in 2018, under the guidance of Prof. Runyao Duan and Prof. Andreas Winter. In 2014, Prof. Wang obtained his B.S. in mathematics (with Wu Yuzhang Honor) from Sichuan University.

PhD Student
I obtained my BS and MS degrees in physics from the University of Melbourne. My research interests include distributed quantum computing, quantum entanglement and quantum machine learning.

PhD Student
I obtained my BS in Applied Mathematics from China Agricultural University under the supervision of Prof. Zhencai Shen. I obtained my MS degree in Cyberspace Security from University of Chinese Academy of Sciences under the supervision of Prof. Zhenyu Huang. My research interests include quantum information theory and quantum computation.
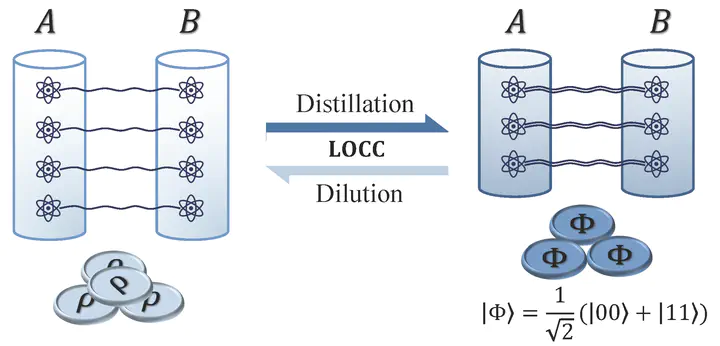 The sketch of entanglement manipulation assisted with LOCC.
The sketch of entanglement manipulation assisted with LOCC.