Abstract
We introduce a reversible theory of exact entanglement manipulation by establishing a necessary and sufficient condition for state transfer under trace-preserving transformations that completely preserve the positivity of partial transpose (PPT). Under these free transformations, we show that logarithmic negativity emerges as the pivotal entanglement measure for determining entangled states’ transformations, analogous to the role of entropy in the second law of thermodynamics. Previous results have proven that entanglement is irreversible under quantum operations that completely preserve PPT and leave open the question of reversibility for quantum operations that do not generate entanglement asymptotically. However, we find that going beyond the complete positivity constraint imposed by standard quantum mechanics enables a reversible theory of exact entanglement manipulation, which may suggest a potential incompatibility between the reversibility of entanglement and the fundamental principles of quantum mechanics.
Publication
arXiv:2312.04456

Associate Professor
Prof. Xin Wang founded the QuAIR lab at HKUST(Guangzhou) in June 2023. His research primarily focuses on better understanding the limits of information processing with quantum systems and the power of quantum artificial intelligence. Prior to establishing the QuAIR lab, Prof. Wang was a Staff Researcher at the Institute for Quantum Computing at Baidu Research, where he concentrated on quantum computing research and the development of the Baidu Quantum Platform. Notably, he spearheaded the development of Paddle Quantum, a Python library designed for quantum machine learning. From 2018 to 2019, Prof. Wang held the position of Hartree Postdoctoral Fellow at the Joint Center for Quantum Information and Computer Science (QuICS) at the University of Maryland, College Park. He earned his doctorate in quantum information from the University of Technology Sydney in 2018, under the guidance of Prof. Runyao Duan and Prof. Andreas Winter. In 2014, Prof. Wang obtained his B.S. in mathematics (with Wu Yuzhang Honor) from Sichuan University.

Research Associate
I obtained my BS in Mathematics and Applied Mathematics from University of Science and Technology of China. I obtained my PhD degree in Applied Mathematics from University of Chinese Academy of Sciences under the supervision of Prof. Xiao-Shan Gao. My research interests include quantum computing, symbolic computation and cryptanalysis.

PhD Student
I obtained my BMath in AMath, CO & joint PMath from the University of Waterloo. My research interests include quantum information theory and quantum machine learning.

PhD Student
I obtained my BS and MS degrees in computer science from the University of Melbourne. My research interests include distributed quantum computing, quantum entanglement and quantum machine learning.
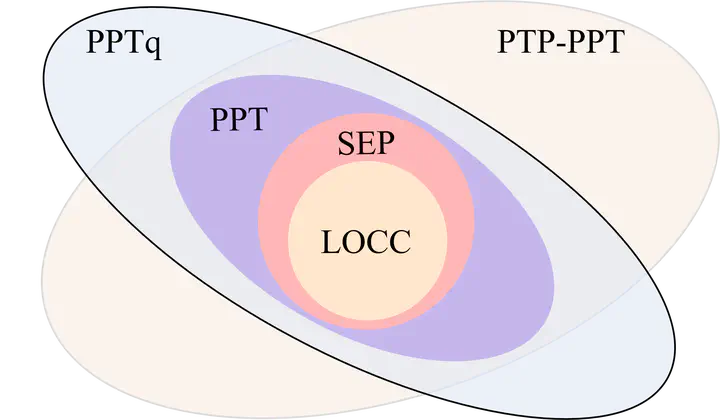 Schematic hierarchy of operations.
Schematic hierarchy of operations.