Overview of PQCs for approximating continuous functions.Abstract
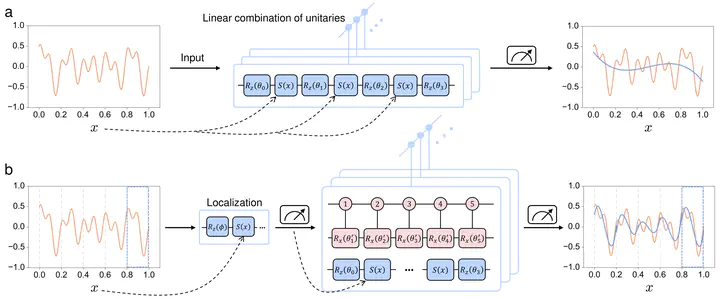
Understanding the power of parameterized quantum circuits (PQCs) in accomplishing machine learning tasks is one of the most important questions in quantum machine learning. In this paper, we analyze the expressivity of PQCs through the lens of function approximation. Previously established universal approximation theorems for PQCs are mainly nonconstructive, leading us to the following question: How large do the PQCs need to be to approximate the target function up to a given error? We exhibit explicit constructions of data re-uploading PQCs for approximating continuous and smooth functions and establish quantitative approximation error bounds in terms of the width, the depth and the number of trainable parameters of the PQCs. To achieve this, we utilize techniques from quantum signal processing and linear combinations of unitaries to construct PQCs that implement multivariate polynomials. We implement global and local approximation techniques using Bernstein polynomials and local Taylor expansion and analyze their performances in the quantum setting. We also compare our proposed PQCs to nearly optimal deep neural networks in approximating high-dimensional smooth functions, showing that the ratio between model sizes of PQC and deep neural networks is exponentially small with respect to the input dimension. This suggests a potentially novel avenue for showcasing quantum advantages in quantum machine learning.
Xin Wang
Associate Professor
Prof. Xin Wang founded the QuAIR lab at HKUST(Guangzhou) in June 2023. His research primarily focuses on better understanding the limits of information processing with quantum systems and the power of quantum artificial intelligence. Prior to establishing the QuAIR lab, Prof. Wang was a Staff Researcher at the Institute for Quantum Computing at Baidu Research, where he concentrated on quantum computing research and the development of the Baidu Quantum Platform. Notably, he spearheaded the development of Paddle Quantum, a Python library designed for quantum machine learning. From 2018 to 2019, Prof. Wang held the position of Hartree Postdoctoral Fellow at the Joint Center for Quantum Information and Computer Science (QuICS) at the University of Maryland, College Park. He earned his doctorate in quantum information from the University of Technology Sydney in 2018, under the guidance of Prof. Runyao Duan and Prof. Andreas Winter. In 2014, Prof. Wang obtained his B.S. in mathematics (with Wu Yuzhang Honor) from Sichuan University.