Abstract
The manipulation of quantum states through linear maps beyond quantum operations has many important applications in various areas of quantum information processing. Current methods simulate unphysical maps by sampling physical operations, but in a classical way. In this work, we show that using quantum measurement in place of classical sampling leads to lower simulation costs for general Hermitian-preserving maps. Remarkably, we establish the equality between the simulation cost and the well-known diamond norm, thus closing a previously known gap and assigning diamond norm a universal operational meaning as a map’s simulability. We demonstrate our method in two applications closely related to error mitigation and quantum machine learning, where it exhibits a favorable scaling. These findings highlight the power of quantum measurement in simulating unphysical operations, in which quantum interference is believed to play a vital role. Our work paves the way for more efficient sampling techniques and has the potential to be extended to more quantum information processing scenarios.
Publication
arXiv.2309.09963

PhD Student
I obtained my BMath in AMath, CO & joint PMath from the University of Waterloo. My research interests include quantum information theory and quantum machine learning.

Research Assistant
I obtained my MS degree in Physics from Imperial College London. I was an intern at Baidu Research under the supervision of Prof. Xin Wang. I am currently a PhD student in quantum information at Osaka University. My research interests include quantum error mitigation, quantum information theory and quantum computation.

Associate Professor
Prof. Xin Wang founded the QuAIR lab at HKUST(Guangzhou) in June 2023. His research primarily focuses on better understanding the limits of information processing with quantum systems and the power of quantum artificial intelligence. Prior to establishing the QuAIR lab, Prof. Wang was a Staff Researcher at the Institute for Quantum Computing at Baidu Research, where he concentrated on quantum computing research and the development of the Baidu Quantum Platform. Notably, he spearheaded the development of Paddle Quantum, a Python library designed for quantum machine learning. From 2018 to 2019, Prof. Wang held the position of Hartree Postdoctoral Fellow at the Joint Center for Quantum Information and Computer Science (QuICS) at the University of Maryland, College Park. He earned his doctorate in quantum information from the University of Technology Sydney in 2018, under the guidance of Prof. Runyao Duan and Prof. Andreas Winter. In 2014, Prof. Wang obtained his B.S. in mathematics (with Wu Yuzhang Honor) from Sichuan University.
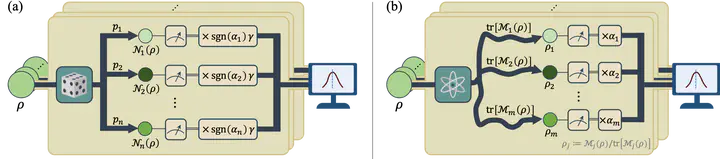 Difference between (a) quasi-probability decomposition and (b) measurement-controlled post-processing.
Difference between (a) quasi-probability decomposition and (b) measurement-controlled post-processing.