Entanglement Distillation -- DEJMPS Protocol¶

Copyright (c) 2021 Institute for Quantum Computing, Baidu Inc. All Rights Reserved.

Overview¶

Before reading this tutorial, we highly recommend you to read the BBPSSW protocol first if you are not familiar with entanglement distillation. The DEJMPS protocol, introduced by Deutsch et al. [1], is similar to the BBPSSW protocol. The main difference between these two protocols is the state for distillation: the DEJMPS protocol can distill Bell-diagonal states, while the BBPSSW protocol could distill isotropic states. In entanglement distillation, the main purpose is to generate a maximally entangled state |Φ+⟩|Φ+⟩ from many copies of imperfect entangled states, using only LOCC operations. Recall the four Bell states,

|Φ±⟩AB=1√2(|0⟩A⊗|0⟩B±|1⟩A⊗|1⟩B),|Ψ±⟩AB=1√2(|0⟩A⊗|1⟩B±|1⟩A⊗|0⟩B),(1)|Φ±⟩AB=12(|0⟩A⊗|0⟩B±|1⟩A⊗|1⟩B),(1)|Ψ±⟩AB=12(|0⟩A⊗|1⟩B±|1⟩A⊗|0⟩B),

where AA and BB represent the bi-party Alice and Bob. The Bell-diagonal state, by definition, is diagonal in the Bell basis that can be expressed as

ρdiag=p1|Φ+⟩⟨Φ+|+p2|Ψ+⟩⟨Ψ+|+p3|Φ−⟩⟨Φ−|+p4|Ψ−⟩⟨Ψ−|,(2)(2)ρdiag=p1|Φ+⟩⟨Φ+|+p2|Ψ+⟩⟨Ψ+|+p3|Φ−⟩⟨Φ−|+p4|Ψ−⟩⟨Ψ−|,

with p1>p2≥p3≥p4p1>p2≥p3≥p4 and p1+p2+p3+p4=1p1+p2+p3+p4=1. Then the entanglement quantification of a Bell-diagonal state can be described as:

  • State fidelity F=⟨Φ+|ρdiag|Φ+⟩=p1F=⟨Φ+|ρdiag|Φ+⟩=p1
  • Negativity N(ρdiag)=p1−1/2N(ρdiag)=p1−1/2

Note: The Bell-diagonal state is distillable when p1>1/2p1>1/2.

DEJMPS protocol¶

Suppose that two parties, namely Alice(AA) and Bob(BB), possess two copies of entangled qubit: {A0,B0},{A1,B1}{A0,B0},{A1,B1}. If these two pairs are all in the same Bell-diagonal state ρdiagρdiag, with p1>0.5p1>0.5. We can apply the following workflow to purify the input states and obtain an output state that has a fidelity closer to |Φ+⟩|Φ+⟩:

  1. Alice and Bob firstly choose the qubit pair they want to keep as the memory qubit pair after distillation. Here, they choose A0A0 and B0B0.
  2. Alice performs Rx(π/2)Rx(π/2) gates on both qubits, and Bob performs Rx(−π/2)Rx(−π/2) gates on both qubits.
  3. Then, Alice and Bob both apply a CNOT gate on their qubits. Here, they choose A0,B0A0,B0 as the control qubits and A1,B1A1,B1 as the target qubits.
  4. Two remote parties measure the target qubits and use a classical communication channel to exchange their measurement results mA1,mB1mA1,mB1.
  5. If the measurement results of Alice and Bob are the same (00 or 11), the distillation is successful, and the qubit pair A0,B0A0,B0 is stored as state ρoutρout; If the measurement results are different (01 or 10), they claim the distillation failed and the qubit pair A0,B0A0,B0 will be discarded.
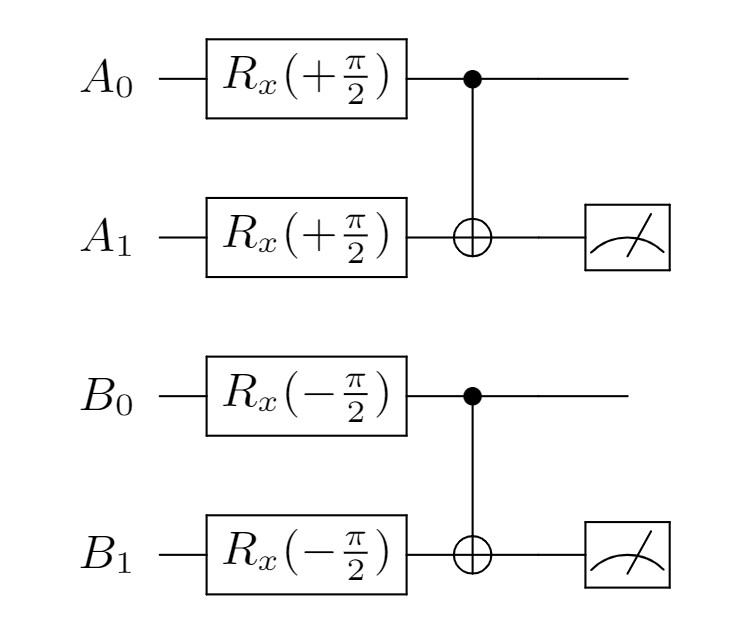
No description has been provided for this image
Figure 1: Schematic diagram of the DEJMPS protocol

After the distillation, the final state ρoutρout of entangled pair A0,B0A0,B0 will have a higher fidelity than the initial state ρρ. The fidelity of the final state FoutFout is

Fout=p21+p24(p1+p4)2+(p2+p3)2.(3)(3)Fout=p12+p42(p1+p4)2+(p2+p3)2.

Similar to the BBPSSW protocol, the DEJMPS protocol is probabilistic, with the probability of a successful distillation being

psucc=(p1+p4)2+(p2+p3)2.(4)(4)psucc=(p1+p4)2+(p2+p3)2.

Simulation with Paddle Quantum¶

First, we need to import relevant packages:

In [2]:
import numpy as np
import paddle
from paddle import matmul, trace
import paddle_quantum
from paddle_quantum.locc import LoccNet
from paddle_quantum.state import bell_state, isotropic_state, bell_diagonal_state
from paddle_quantum.qinfo import negativity, logarithmic_negativity, is_ppt
# Change to density matrix mode
paddle_quantum.set_backend('density_matrix')

Let us see the theoretical result of applying the DEJMPS protocol to the state

ρ=p1|Φ+⟩⟨Φ+|+1−p12|Ψ+⟩⟨Ψ+|+1−p13|Φ−⟩⟨Φ−|+1−p16|Ψ−⟩⟨Ψ−|.(5)(5)ρ=p1|Φ+⟩⟨Φ+|+1−p12|Ψ+⟩⟨Ψ+|+1−p13|Φ−⟩⟨Φ−|+1−p16|Ψ−⟩⟨Ψ−|.

Suppose we take p1=0.7p1=0.7, then the theoretical improvement of fidelity can be calculated by the following block:

In [3]:
def DEJMPS_metrics(*p):
    """
    Returns output fidelity and probability of success of the DEJMPS protocol.
    """
    F_in = p[0]
    p_succ = (p[0] + p[3]) ** 2 + (p[1] + p[2]) ** 2
    F_out = (p[0] ** 2 + p[3] ** 2)/p_succ

    return F_in, F_out, p_succ

p = 0.7
F_in, F_out, p_succ = DEJMPS_metrics(p, (1-p)/2, (1-p)/3, (1-p)/6)
print("The input fidelity is:", F_in)
print("The output fidelity is:", F_out)
print("With a probability of success:", p_succ)
print("The input state satisfies the PPT condition and hence not distillable?", 
      is_ppt(bell_diagonal_state([p, (1-p)/2, (1-p)/3, (1-p)/6])))

The input fidelity is: 0.7
The output fidelity is: 0.7879999999999999
With a probability of success: 0.625
The input state satisfies the PPT condition and hence not distillable? False

Then we can simulate the DEJMPS protocol and check if the results match with the theory.

In [4]:
class LOCC(LoccNet):
    def __init__(self):
        super(LOCC, self).__init__()
        # Add the first party Alice 
        # The first parameter 2 stands for how many qubits A holds
        # The second parameter records the name of this party
        self.add_new_party(2, party_name='Alice')
        # Add the second party Bob
        # The first parameter 2 stands for how many qubits A holds
        # The second parameter records the name of this party
        self.add_new_party(2, party_name='Bob')

        # Define the input quantum states rho_in
        _state = bell_diagonal_state([p, (1-p)/2, (1-p)/3, (1-p)/6])
        # ('Alice', 0) means Alice's first qubit A0
        # ('Bob', 0) means Bob's first qubit B0
        self.set_init_state(_state, [('Alice', 0), ('Bob', 0)])
        # ('Alice', 1) means Alice's second qubit A1
        # ('Bob', 1) means Bob's second qubit B1
        self.set_init_state(_state, [('Alice', 1), ('Bob', 1)])

        # Set the angles of the Rx gates
        self.theta1 = paddle.to_tensor([np.pi/2, np.pi/2])
        self.theta2 = paddle.to_tensor([-np.pi/2, -np.pi/2])

        # Create Alice's local operations 
        self.cir1 = self.create_ansatz('Alice')
        self.cir1.rx(qubits_idx=0, param=self.theta1[0])
        self.cir1.rx(qubits_idx=1, param=self.theta1[1])
        self.cir1.cnot([0, 1])
        # Create Bob's local operations 
        self.cir2 = self.create_ansatz('Bob')
        self.cir2.rx(qubits_idx=0, param=self.theta2[0])
        self.cir2.rx(qubits_idx=1, param=self.theta2[1])
        self.cir2.cnot([0, 1])

    def DEJMPS(self):
        status = self.init_status
        # Run circuit
        status = self.cir1(status)
        status_mid = self.cir2(status)

        # ('Alice', 1) means measuring Alice's second qubit A1
        # ('Bob', 1) means measuring Bob's second qubit B1
        # ['00','11'] specifies the success condition for distillation
        # Means Alice and Bob both measure '00' or '11'
        status_mid = self.measure(status_mid, [('Alice', 1), ('Bob', 1)], ["00", "11"])

        # Trace out the measured qubits A1&B1
        # Leaving only Alice’s first qubit and Bob’s first qubit A0&B0 as the memory register
        status_fin = self.partial_state(status_mid, [('Alice', 0), ('Bob', 0)])

        return status_fin
In [6]:
# Run DEJMPS protocol
status_fin = LOCC().DEJMPS()

# Calculate fidelity
target_state = bell_state(2)
fidelity = 0
for status in status_fin:
    fidelity += paddle.real(trace(matmul(target_state.data, status.data)))
fidelity /= len(status_fin)

# Calculate success rate
suc_rate = sum([status.prob for status in status_fin])

# Output simulation results
print(f"The fidelity of the input quantum state is: {p:.5f}")
print(f"The fidelity of the purified quantum state is: {fidelity.numpy()[0]:.5f}")
print(f"The probability of successful purification is: {suc_rate.numpy()[0]:#.3%}")

# Print the output state
rho_out = status_fin[0]
print("========================================================")
print(f"The output state is:\n {np.around(rho_out.data.numpy(), 4)}")
print(f"The initial negativity is: {negativity(bell_diagonal_state([p, (1-p)/2, (1-p)/3, (1-p)/6])).numpy()[0]}")
print(f"The final negativity is: {negativity(rho_out).numpy()[0]}")

The fidelity of the input quantum state is: 0.70000
The fidelity of the purified quantum state is: 0.78800
The probability of successful purification is: 62.500%
========================================================
The output state is:
 [[0.45 +0.j 0.   +0.j 0.   +0.j 0.338+0.j]
 [0.   +0.j 0.05 +0.j 0.002+0.j 0.   +0.j]
 [0.   +0.j 0.002+0.j 0.05 +0.j 0.   +0.j]
 [0.338+0.j 0.   +0.j 0.   +0.j 0.45 +0.j]]
The initial negativity is: 0.19999995827674866
The final negativity is: 0.28800004720687866

One can observe that the simulation result is in exact accordance with the theoretical values.

Conclusion¶

The DEJMPS protocol can effectively extract one entangled pair with a higher fidelity from two noisy pairs. And compared to the BBPSSW protocol [2], it can be applied to Bell-diagonal states instead of isotropic states. Note that isotropic state is a special case of Bell-diagonal state. So in this sense, the DEJMPS protocol is more general than the BBPSSW protocol. However, it also shares the same disadvantages of the BBPSSW protocol including the limited type of input states and poor scalability.

Next, We suggest interested readers to check the tutorial on how to design a new distillation protocol with LOCCNet.

References¶

[1] Deutsch, David, et al. "Quantum privacy amplification and the security of quantum cryptography over noisy channels." Physical Review Letters 77.13 (1996): 2818.

[2] Bennett, Charles H., et al. "Purification of noisy entanglement and faithful teleportation via noisy channels." Physical Review Letters 76.5 (1996): 722.