Learning the Quantum Teleportation Protocol¶

Copyright (c) 2021 Institute for Quantum Computing, Baidu Inc. All Rights Reserved.

Overview¶

Quantum teleportation is another important task that can be completed by Local Operations and Classical Communication (LOCC) protocols, which transfers quantum information between two spatially separated communication nodes (only classical communication channel allowed) with the help of entanglement. In this tutorial, we will first briefly review the original teleportation protocol and simulate it with Paddle Quantum. Then, we will go through how to learn a teleportation protocol with LOCCNet.

The original quantum teleportation protocol¶

The original teleportation protocol was proposed by C. H. Bennett et al. in 1993 [1] and experimentally verified in 1997 with photonic platforms [2-3]. The workflow is illustrated in the figure below. Following the convention, this process requires 2 communication nodes or parties, namely $A$ (Alice) and $B$ (Bob). For simplicity, we only consider transferring a single-qubit quantum state $|\psi\rangle_C$ and this requires 3 qubits in total including the pre-shared maximally entangled state $|\Phi^+\rangle_{AB} = \frac{1}{\sqrt{2}}(|00\rangle + |11\rangle)$. Alice holds systems A and C，Bob holds system B. Note: Only quantum information is transferred, not the physical qubits.

teleportation

Figure 1: Quantum teleportation: Transferring quantum state $|\psi\rangle$ from Alice to receiver Bob.

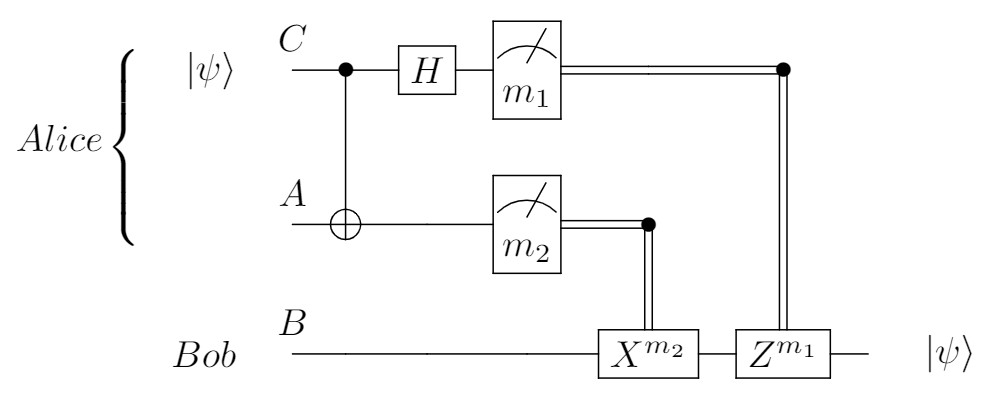
Step I: At the very beginning, the system state can be described as

$$ \lvert\varphi_{0}\rangle = \lvert\psi\rangle_{C}\otimes \lvert\Phi^+\rangle_{AB} = \frac{1}{\sqrt{2}}\big[\alpha\lvert0\rangle(\lvert00\rangle + \lvert11\rangle)+\beta\lvert1\rangle(\lvert00\rangle + \lvert11\rangle)\big], \tag{1} $$

where the quantum state Alice want to transmit is $|\psi\rangle_C = \alpha|0\rangle_C + \beta|1\rangle_C$ and the coefficients $\alpha, \beta \in \mathbb{C}$.

Step II: Alice applies a CNOT gate, and the resulting state is

$$ |\varphi_1\rangle = \frac{1}{\sqrt{2}}\big[\alpha\lvert0\rangle(\lvert00\rangle + \lvert11\rangle)+\beta\lvert1\rangle(\lvert10\rangle + \lvert01\rangle)\big], \tag{2} $$

Step III: Alice applies a Hadamard gate, and the system state becomes $|\varphi_2\rangle$

$$ |\varphi_2\rangle = \frac{1}{2}\big[\alpha(\lvert0\rangle + \lvert1\rangle)(\lvert00\rangle + \lvert11\rangle)+\beta(\lvert0\rangle - \lvert1\rangle)(\lvert10\rangle + \lvert01\rangle)\big], \tag{3} $$

The above state can be rearranged to

$$ \lvert\varphi_{2}\rangle = \frac{1}{2}\big[\lvert00\rangle(\alpha\lvert0\rangle + \beta\lvert1\rangle) + \lvert01\rangle(\alpha\lvert1\rangle + \beta\lvert0\rangle) + \lvert10\rangle(\alpha\lvert0\rangle - \beta\lvert1\rangle) + \lvert11\rangle(\alpha\lvert1\rangle - \beta\lvert0\rangle)\big]. \tag{4} $$

Step IV: Alice measures both of her qubits in the computational basis $\{|00\rangle, |01\rangle, |10\rangle, |11\rangle\}$ and send the results $m_1m_2$ to Bob with a classical channel. There are 4 distinct possibilities: $m_1m_2 \in \{ 00, 01,10, 11\}$. Then, Bob implements certain operations correspondingly on his qubit based on the received messages.

  • If the measurement result is $m_1m_2 = 00$, Bob's state will be $\alpha\lvert0\rangle + \beta\lvert1\rangle$, which is the state Alice want to transmit $\lvert\psi\rangle_C$. No operations are needed and the teleportation is finished.
  • If the measurement result is $m_1m_2 = 01$, Bob's state will be $\alpha\lvert1\rangle + \beta\lvert0\rangle$. Bob needs to act the $X$ gate on his qubit.
  • If the measurement result is $m_1m_2 = 10$, Bob's state will be $\alpha\lvert0\rangle - \beta\lvert1\rangle$. Bob needs to act the $Z$ gate on his qubit.
  • If the measurement result is $m_1m_2 = 11$, Bob's state will be $\alpha\lvert1\rangle - \beta\lvert0\rangle$. Bob needs to act the $X$ gate followed by the $Z$ gate on his qubit.

In the next section, we will go through how to simulate the teleportation protocol with Paddle Quantum.

Simulation with Paddle Quantum¶

First, we need to import all the dependencies:

In [2]:
import numpy as np
import paddle
from paddle import matmul, trace
import paddle_quantum
from paddle_quantum.locc import LoccNet
from paddle_quantum.qinfo import state_fidelity
from paddle_quantum.state import bell_state, isotropic_state, random_state
# Change to density matrix mode
paddle_quantum.set_backend('density_matrix')

Initialize the quantum state, and define the quantum circuit and teleportation protocol.

In [3]:
class LOCC(LoccNet):
    def __init__(self):
        super(LOCC, self).__init__()
        # Add the first party Alice 
        # The first parameter 2 stands for how many qubits A holds
        # The second parameter records the name of this party
        self.add_new_party(2, party_name="Alice")
        # Add the second party Bob
        # The first parameter 1 stands for how many qubits B holds
        # The second parameter records the name of this party
        self.add_new_party(1, party_name="Bob")

        # Create a bell state
        _state = bell_state(2)
        # _state = isotropic_state(2, 0.8)
        # Generate random pure quantum states for teleportation
        self.state_C = random_state(num_qubits=1, rank=1)

        # Initialize the system by distributing states between Alice and Bob
        # ("Alice", 0) refers to qubit C
        # ("Alice", 1) refers to qubit A
        # ("Bob", 0) refers to qubit B
        # print('Pre-shared entanglement state is:\n', _state.numpy())
        self.set_init_state(self.state_C, [("Alice", 0)])
        self.set_init_state(_state, [("Alice", 1), ("Bob", 0)])

        # Create Alice's local operations 
        self.cirA = self.create_ansatz("Alice")
        self.cirA.cnot([0, 1])
        self.cirA.h(0)
        # Create Bob's local operations
        self.cirB = [self.create_ansatz("Bob") for _ in range(4)]
        self.cirB[1].x(0)
        self.cirB[2].z(0)
        self.cirB[3].x(0)
        self.cirB[3].z(0)

    def teleportation(self):
        status = self.init_status
        # Run circuit
        status = self.cirA(status)
        # Alice measures both of her qubits C and A
        status_A = self.measure(status, [("Alice", 0), ("Alice", 1)], ["00", "01", "10", "11"])

        # Record average fidelity 
        fid_list = []
        # Bob applies different gates on his qubits depending on the measurement result of Alice
        for i, s in enumerate(status_A):
            # Bob's circuit
            cirB = self.cirB[int(status_A[i].measured_result, 2)]
            # Run circuit
            status_B = cirB(s) 
            # Trace out the measured qubits C and A
            # Leaving out only Bob’s qubit B
            status_fin = self.partial_state(status_B, [("Bob", 0)])
            # Calculate the fidelity between the teleported state and the original state
            fid = state_fidelity(self.state_C, status_fin) ** 2
            fid_list.append(fid * status_fin.prob)
        fid_avg = sum(fid_list)

        return fid_avg

Then we randomly generate 200 pure quantum states and use state fidelity $F$ to benchmark the teleportation protocol, where

$$ F(\rho,\sigma) \equiv \text{tr}\big( \sqrt{\sqrt{\rho}\sigma \sqrt{\rho}} \big)^2. \tag{5} $$
In [5]:
SEED = 999              # Fix random seed
num_state = 200         # Number of random states generated
list_fid = []           # Record the fidelity
np.random.seed(SEED)
# Start sampling
for idx in range(num_state):
    list_fid.append(LOCC().teleportation().numpy())

print('Teleportation_Fidelity_Avg:', np.around(sum(list_fid)[0] / len(list_fid), 4), ', std=', np.std(list_fid))

Teleportation_Fidelity_Avg: 1.0 , std= 3.9433777e-07

Note: We want to point out the validity of this protocol relies on the quality of the pre-shared entanglement. Readers can change the entangled state from bell_state(2) to isotropic_state(2, p) and see how quantum noises will influence the teleportation performance. Recall the definition of isotropic states,

$$ \rho_{\text{iso}}(p) = p\lvert\Phi^+\rangle \langle\Phi^+\rvert + (1-p)\frac{I}{4}, \quad p \in [0,1] \tag{6} $$

Learning a teleportation protocol with LOCCNet¶

Training the protocol¶

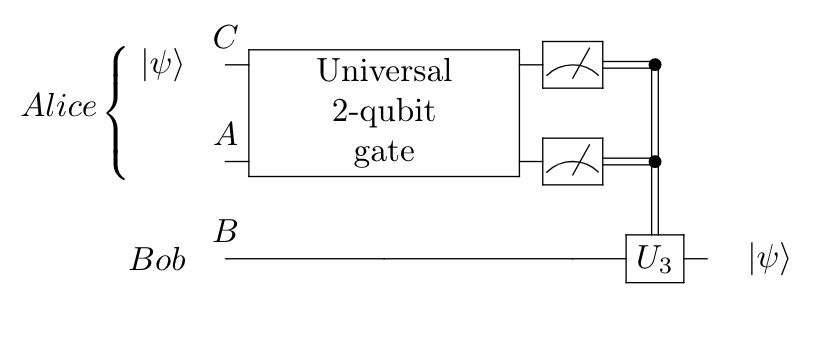
A general LOCC protocol can be classified by the number of classical communication rounds $r$. The original teleportation protocol is a one-round ($r=1$) protocol. For simplicity, we also restrict the communication rounds to 1. Compare to the original protocol, we use parametrized quantum circuits (PQC) to replace the fixed gates $U\in\{X,Z\}$ Bob applied on his qubit with a general rotation gate $U_3$ on the Bloch sphere.

$$ U_3(\theta, \phi, \varphi) = \begin{bmatrix} \cos(\frac{\theta}{2}) & -e^{i\varphi}\sin(\frac{\theta}{2})\\ e^{i\phi}\sin(\frac{\theta}{2}) & e^{i(\phi+\varphi)} \cos(\frac{\theta}{2}) \end{bmatrix}. \tag{7} $$

This would bring us a more powerful searching capability in finding practical LOCC protocols. Similarly, we change Alice's local operations to a more general PQC called the universal_two_qubits() [4]. We summarize the workflow below:

  1. Alice applies a 2-qubit PQC on her qubits.
  2. Alice measures both of her qubits in the computational basis and communicates with Bob through a classical channel.
  3. There are 4 possible measurement results: $m_1m_2 \in \{00, 01, 10, 11\}$. Bob needs to act different operations corresponding to these measurement results. After Bob's local operations, the state on his qubit collapses to $\lvert \psi\rangle_{B}$.
  4. Calculate the overlap $O$ between $\lvert \psi\rangle_{B}$ and $\lvert\psi_C\rangle$ (pure states). LOCCNet framework only supports density matrix formulation and hence we have to rewrite them as $\rho_{B} = |\psi\rangle\langle\psi|_B$ and $\rho_{C} = |\psi\rangle\langle\psi|_C$. Then, $O = \text{Tr}(\rho_C\rho_{B})$. For pure states, this metric is simply the state fidelity.
  5. Set the accumulated loss function over 4 possible measurement results as $L = \sum_{m_1m_2} \big(1-\text{Tr}(\rho_C\rho_{B})\big)$, and use gradient-based optimization methods to update circuit parameters and hence minimize the loss function.
  6. Repeat steps 1-5 until the loss function converges to the global minimum.
  7. Generate an ensemble of arbitrary states $\{\lvert\psi_C\rangle\}$, and benchmark the trained protocol with average state fidelity.

teleportation-LOCCNet

Figure 2: Learning a teleportation protocol with LOCCNet.

Note: In order to make sure the parameters in parameterized quantum circuit is valid for all state after training, we set the training set as 4 linear independent states, which is $\{|0\rangle\langle 0|,|1\rangle\langle 1|,|+\rangle\langle +|,|+\rangle\langle +|_y\}$ or in the density matrix form:

$$ \rho_0 = \left[\begin{array}{ccc} 1 & 0\\ 0 & 0 \end{array}\right], \rho_1 = \left[\begin{array}{ccc} 0 & 0\\ 0 & 1 \end{array}\right], \rho_2 = \left[\begin{array}{ccc} 0.5 & 0.5\\ 0.5 & 0.5 \end{array}\right], \rho_3 = \left[\begin{array}{ccc} 0.5 & -0.5 i\\ 0.5i & 0.5 \end{array}\right]. \tag{8} $$

Any single qubit state can be written as a combination of the above 4 linear independent states in $\mathcal{H}^{2\times 2}$.

In [6]:
class LOCC_Train(LoccNet):
    def __init__(self):
        super(LOCC_Train, self).__init__()
        # Add the first party Alice 
        # The first parameter 2 stands for how many qubits A holds
        # The second parameter records the name of this party
        self.add_new_party(2, party_name="Alice")
        # Add the second party Bob
        # The first parameter 1 stands for how many qubits B holds
        # The second parameter records the name of this party
        self.add_new_party(1, party_name="Bob")

        # Create a bell state
        _state = bell_state(2)
        # _state = isotropic_state(2, 0.8)
        # Training set: 4 linear independent states
        _state0 = paddle_quantum.State(np.array([[1, 0], [0, 0]], dtype=np.complex64))
        _state1 = paddle_quantum.State(np.array([[0, 0], [0, 1]], dtype=np.complex64))
        _state2 = paddle_quantum.State(np.array([[0.5, 0.5], [0.5, 0.5]], dtype=np.complex64))
        _state3 = paddle_quantum.State(np.array([[0.5, -0.5j], [0.5j, 0.5]], dtype=np.complex64))
        self.init_states = [_state0, _state1, _state2, _state3]
        # Initialize the system by distributing states between Alice and Bob
        self.set_init_state(_state, [("Alice", 1), ("Bob", 0)])
        self.set_init_state(_state0, [("Alice", 0)])

        # Define Alice's local operations
        self.cirA = self.create_ansatz("Alice")
        self.cirA.universal_two_qubits([0, 1])
        # Define Bob's local operations
        self.cirB = [self.create_ansatz("Bob") for _ in range(4)]
        for cir in self.cirB:
            # Apply a universal single qubit gate
            cir.u3(0)

    def LOCCNet(self):
        # Define the training process
        loss = 0
        temp_state = self.init_status
        # Training
        for init_state in self.init_states:
            # Reset Alice's first qubit C to states in training set
            status = self.reset_state(temp_state, init_state, [("Alice", 0)])
            # Run circuit
            status = self.cirA(status)
            # Obtain 4 possible measurement results
            status_A = self.measure(status, [("Alice", 0), ("Alice", 1)], ["00", "01", "10", "11"])

            # Bob needs to apply different operation on his qubits, depending on the measurement results
            for i, s in enumerate(status_A):
                # Run circuit
                status_B = self.cirB[i](s)
                # Trace out the measured qubits C and A
                # Leaving out only Bob’s qubit B
                status_fin = self.partial_state(status_B, [("Bob", 0)])
                # Summing up the loss function for all possible measurement results
                loss += 1 - paddle.real(trace(matmul(init_state.data, status_fin.data)))

        return loss

    # Save the optimized parameters
    def save_module(self):
        theta_A = self.cirA.parameters()
        theta_B = [self.cirB[i].parameters() for i in range(4)]
        theta = theta_A + sum(theta_B, [])
        paddle.save(theta, 'parameters/QT_LOCCNet')
In [8]:
ITR = 150   # Number of iterations
LR = 0.2    # Set up learning rate
SEED = 999  # Fix random seed for parameters in PQC
np.random.seed(SEED)
paddle.seed(SEED)

net = LOCC_Train()
params = net.cirA.parameters() + sum([net.cirB[i].parameters() for i in range(4)], [])
# Choose the Adam optimizer
opt = paddle.optimizer.Adam(learning_rate=LR, parameters=params)
# Optimization loop
for itr in range(ITR):
    # Forward propagation to calculate loss function
    loss = net.LOCCNet()
    # Backpropagation
    loss.backward()
    opt.minimize(loss)
    # Clean gradients
    opt.clear_grad()
    if itr % 10 == 0:
        print("itr " + str(itr) + ":", loss.numpy()[0])

# Save parameters
net.save_module()

itr 0: 7.721435
itr 10: 0.5636051
itr 20: 0.20643002
itr 30: 0.073403895
itr 40: 0.025113285
itr 50: 0.008655369
itr 60: 0.0035846233
itr 70: 0.0014438629
itr 80: 0.00045502186
itr 90: 0.00018626451
itr 100: 4.7028065e-05
itr 110: 1.4960766e-05
itr 120: 4.4703484e-06
itr 130: 3.1590462e-06
itr 140: 1.66893e-06

Benchmark¶

If you don't want to spend time on training, you can load the pre-trained circuit parameters and directly test the performance.

In [9]:
class LOCC_Test(LoccNet):
    def __init__(self, theta_A, theta_B):
        super(LOCC_Test, self).__init__()
        self.parties = list()
        self.add_new_party(2, party_name="Alice")
        self.add_new_party(1, party_name="Bob")

        _state = bell_state(2)
        self._state0 = random_state(1)
        self.set_init_state(_state, [("Alice", 1), ("Bob", 0)])
        self.set_init_state(self._state0, [("Alice", 0)])

        self.cirA = self.create_ansatz("Alice")
        self.cirA.universal_two_qubits(qubits_idx=[0, 1], param=theta_A)
        self.cirB = [self.create_ansatz("Bob") for _ in range(4)]
        for i, cir in enumerate(self.cirB):
            cir.u3(qubits_idx=0, param=theta_B[i])
        

    def benchmark(self):
        input_state = self.init_status
        status = self.cirA(input_state)
        status_A = self.measure(status, [("Alice", 0), ("Alice", 1)], ["00", "01", "10", "11"])
        fid_list = []
        for i, s in enumerate(status_A):
            status_B = self.cirB[i](s)
            status_fin = self.partial_state(status_B, [("Bob", 0)])
            fid = state_fidelity(self._state0, status_fin) ** 2
            fid_list.append(fid * status_fin.prob)
        fid_ave = sum(fid_list)
        
        return fid_ave
In [10]:
# Load pre-trained circuit parameters
para = paddle.load('parameters/QT_LOCCNet')
np.random.seed(999)     # Fix random seed
num_state = 200         # Number of random states generated
list_fid = []           # Record the fidelity
np.random.seed(SEED)
paddle.seed(SEED)

# Start sampling
for idx in range(num_state):
    list_fid.append(LOCC_Test(para[0], para[1:]).benchmark().numpy())

print('LOCCNet_Fidelity_avg:', np.around(sum(list_fid)[0] / len(list_fid), 4), ', std=', np.std(list_fid))

LOCCNet_Fidelity_avg: 1.0 , std= 3.8644316e-07

Conclusion¶

Based on LOCCNet we successfully learned a teleportation protocol with a noiseless pre-shared Bell state. The original teleportation protocol was designed to transfer a single-qubit quantum state. It is not clear how it can be generalize to the multi-qubit case. By comparison, LOCCNet provides the possibility of training a teleportation protocol for multi-qubit quantum states. Also, it will be an interesting question to ask how robust LOCCNet will be against various noises. On the other hand, the teleportation protocol could be viewed as a special case of simulating the identity channel $\mathcal{E}_I$ where Alice sends $\psi$ and Bob receives $\mathcal{E}_I(\psi)$. This idea can be extended to simulate many other channels including the depolarizing channel $\mathcal{E}_{D}$.

References¶

[1] Bennett, Charles H., et al. "Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels." Physical Review Letters 70.13 (1993): 1895.

[2] Boschi, Danilo, et al. "Experimental realization of teleporting an unknown pure quantum state via dual classical and Einstein-Podolsky-Rosen channels." Physical Review Letters 80.6 (1998): 1121.

[3] Bouwmeester, Dik, et al. "Experimental quantum teleportation." Nature 390.6660 (1997): 575-579.

[4] Vidal, Guifre, and Christopher M. Dawson. "Universal quantum circuit for two-qubit transformations with three controlled-NOT gates." Physical Review A 69.1 (2004): 010301.