Data Encoding Analysis¶
Copyright (c) 2022 Institute for Quantum Computing, Baidu Inc. All Rights Reserved.
Overview¶
Many studies are now exhibiting the promise of Variational Quantum Algorithms (VQA) in demonstrating quantum advantages on near-term quantum devices, with particular emphasis on using them to solve supervised learning tasks. VQA is also known as a Parameterized Quantum Circuit (PQC), which is divided into two main parts in this tutorial: the data encoding circuit and the quantum neural network. The data encoding circuit converts classical data into quantum states, and the quality of the quantum states has a direct impact on the classification results. When data encoding is analyzed through the perspective of kernel functions, different encoding methods correspond to different kernel functions, which play a critical role in the classification of quantum states [1,2]. It often determines the expressiveness and generalization ability of the method by analyzing data encoding from the standpoint of statistical learning theory [3,4]. Therefore, it is necessary to conduct a systematic analysis of data encoding. From the standpoint of quantum information, literature [5] critically analyzes the effect of the width and depth of the data encoding circuit on the quantum state.
The next part of the tutorial is organized around the literature [5] and is divided into two parts: theory and Paddle Quantum implementation. The fundamental concepts and main conclusions are introduced first, followed by specific implementation solutions.
Theory¶
Fundamental Concepts¶
Figure 1 shows the flowchart for encoding classical data into quantum states. Assume that the classical data are independent identically distributed samples of distribution $D$, each classical data is $\pmb x$, which becomes a quantum state $\rho(\pmb x)$ after passing through the data encoding circuit. Here the concept of average quantum state over the distribution $D$ is introduced, i.e.
$$ \bar{\rho}:=\mathbf{E}[\rho(\pmb x)]. \tag{1} $$Given a classical data set $S$ consisting of $M$ data, we usually use the average value to approximate the average quantum state of $S$
$$ \bar{\rho}:=\frac{1}{M}\sum_{j=1}^M\rho(\pmb x_j). \tag{2} $$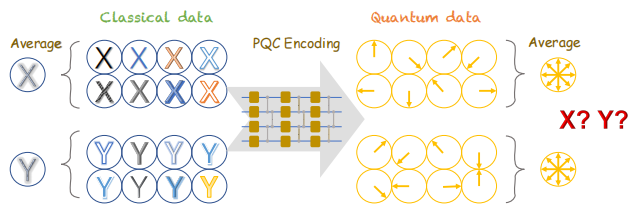
There are various methods for measuring the distance between quantum states, including trace distance, fidelity, Petz-Rényi divergence, and others. In this tutorial, the Petz-Rényi divergence is used as a measure of the distance between different quantum states. Specifically, the Petz-Rényi divergence of the quantum states $\rho_0$ and $\rho_1$ is defined as
$$ D_2(\rho_0||\rho_1)=logTr[\rho_0^2\rho_1^{-1}], \tag{3} $$the closer the two quantum states are, the smaller the value of $D_2$.
Main Result¶
The Petz-Rényi divergence metric is then used to calculate the distance between the encoding average quantum state and the maximum mixed state. It is not difficult to believe that this distance is related to the property of the classical dataset and how the data are encoded. Assume that each feature dimension of the classical dataset satisfies certain independence and has a standard deviation of at least $\sigma$. The following inequality then holds for the encoding circuit depicted in figure 2 (with width and depth $n$ and $D$, respectively)
$$ D_2(\bar{\rho}||I/2^n)\leq log(1+(2^n-1)2^{-D\sigma^2}), \tag{4} $$where $I/2^n$ is the maximum mixed state of $n$ bits and $I$ is the unit matrix.
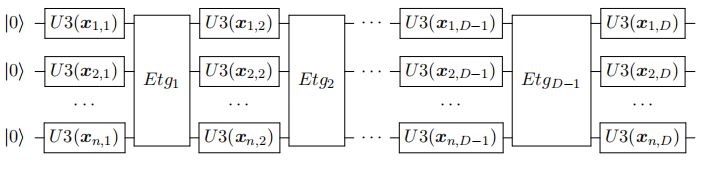
A more rigorous description and proof of the theorem can be found in [5], and the focus of this tutorial will be on what this conclusion implies and illuminates.
This means that the average quantum state converges to the maximum mixed state at an exponential rate as the circuit depth increases. For example, if the average quantum states of both classes 0 and 1 eventually converge to the maximum mixed state, it will be impossible to distinguish the average quantum states of these two classes from the standpoint of quantum information, i.e., it will be impossible to distinguish classical data features in an average sense.
When the classical data features have a high dimensionality (e.g., picture data), angle encoding may not be the best option. This is due to the fact that it can easily lead to very deep encoding circuits, and widening circuits may run into the barren plateau problem, which severely limits VQA's capability. As a result, some dimensionality reduction operations must be performed on the traditional data before it is fed into the circuit.
Paddle Quantum Implementation¶
This section focuses on two experiments using Paddle Quantum on the MNIST dataset:
- Exploring the trend of the Petz-Rényi divergence between the average quantum state and the maximum mixed state with the depth of the data encoding circuit
- Investigate changes in classification accuracy as the data encoding circuit becomes deeper.
First import the relevant packages¶
# import numpy, paddle, and paddle_quantum
import numpy as np
import paddle
import paddle_quantum
# import circuit module
from paddle_quantum.ansatz import Circuit
# import some function
from numpy import pi as PI
from paddle import matmul, transpose, reshape, real, argmax, cast, mean, concat, real
from paddle_quantum.qinfo import pauli_str_to_matrix
from paddle_quantum.linalg import dagger
import paddle.nn.functional as F
# dataset tool
from paddle_quantum.dataset import MNIST
# plot and time module
from matplotlib import pyplot as plt
from pylab import axes
import time
Parameterized Quantum Circuit¶
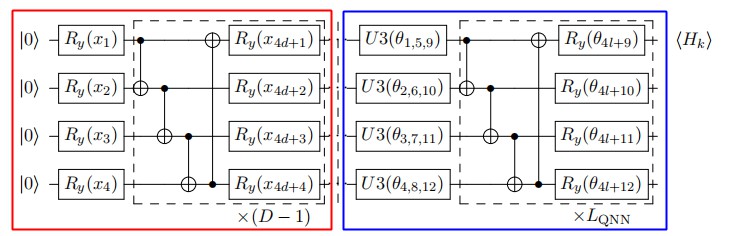
The red box on the left in Figure 3 is the data encoding circuit, a special case of Figure 2, and the blue box on the right is the quantum neural network. The data encoding circuit here is made up of $R_y$ and CNOT, and the specific circuit depth $D$ is determined by the data feature dimension. The MNIST dataset will be used in this tutorial and the images are downscaled to 16-dimensional feature vectors. The number of quantum bits is chosen to be 8, 6, 4, 3, 2, and the corresponding circuit depths are 2, 3, 4, 6, 8. The positions larger than 16 dimensions will be filled with 0, i.e., $R_y(0)$. The quantum neural network part consists of the single-bit universal gate $U3$ and CNOT. The specific circuit depth $L$ can be set freely.
Encoding classical Data into quantum states¶
Here you need the dataset tool dataset provided by Paddle Quantum. The MNIST data are encoded into quantum states using the data encoding circuit shown in Figure 2 before being fed into the quantum neural network for training.
train_data, test_data = [], []
# Binary classification task
classes = [3,6]
training_data_num = 1000
testing_data_num = 200
qubit_num_list = [8, 6, 4, 3, 2]
# Encode classical data using circuits of different widths and depths and save them
for qubit_num in qubit_num_list:
# training dataset
train_dataset = MNIST(mode='train', encoding='real_entangled_encoding', num_qubits=qubit_num,
classes=classes,
data_num=training_data_num,
downscaling_method='resize', target_dimension=16,
need_relabel=True, return_state=True)
# validation dataset
val_dataset = MNIST(mode='test', encoding='real_entangled_encoding', num_qubits=qubit_num,
classes=classes,
data_num=testing_data_num,
downscaling_method='resize', target_dimension=16,
need_relabel=True, return_state=True)
# x and y
train_x, train_y = train_dataset.quantum_image_states, train_dataset.labels
test_x, test_y = val_dataset.quantum_image_states, val_dataset.labels
train_data.append((train_x, train_y))
test_data.append((test_x, test_y))
print(train_data[0][0].shape)
print(train_data[0][1].shape)
print(test_data[0][0].shape)
print(test_data[0][1].shape)
[1000, 256] (1000,) [200, 256] (200,)
Building Quantum Neural Network¶
# Construct model
class Net(paddle.nn.Layer):
"""
construct network
"""
def __init__(self, n, depth):
# Initialize the circuit: n, depth
super(Net, self).__init__()
self.n = n
self.depth = depth
self.circuit = Circuit(n)
# Add layers of rotation gates
for i in range(n):
self.circuit.rz(qubits_idx=i)
self.circuit.ry(qubits_idx=i)
self.circuit.rz(qubits_idx=i)
# default depth = 1
# Add layers of entanglement
for d in range(3, depth + 3):
for i in range(n-1):
self.circuit.cnot(qubits_idx=[i, i + 1])
self.circuit.cnot(qubits_idx=[n-1, 0])
for i in range(n):
self.circuit.ry(qubits_idx=i)
# Define forward propagation mechanism, and then calculate loss function and cross-validation accuracy
def forward(self, state_in, label):
"""
Input:
state_in: input quantum state, shape: [-1, 1, 2^n] -- Here is [BATCH, 1, 2^n]
label: labels of input quantum state, shape: [-1, 1]
Loss function:
The cross entropy loss
"""
# Initialize theta
Utheta = self.circuit.unitary_matrix()
# row vector operations here to speed up
state_out = matmul(state_in, Utheta) # shape [-1, 1, 2 ** n]
# Measure the expected value of the pauli Z operator <Z>
Ob1 = paddle.to_tensor(pauli_str_to_matrix([[1.0, 'z0']], self.n))
E_Ob1 = matmul(matmul(state_out, Ob1), transpose(paddle.conj(state_out), perm=[0, 2, 1]))
E_Ob1_re = reshape(real(E_Ob1), [-1, 1])
Ob2 = paddle.to_tensor(pauli_str_to_matrix([[1.0, 'x0']], self.n))
E_Ob2 = matmul(matmul(state_out, Ob2), transpose(paddle.conj(state_out), perm=[0, 2, 1]))
E_Ob2_re = reshape(real(E_Ob2), [-1, 1])
outputs = concat([E_Ob1_re, E_Ob2_re], axis=-1)
# Calculate loss and accuracy
loss = F.cross_entropy(outputs, label)
acc = mean(cast(argmax(outputs, axis=-1) == label, "float32"))
return loss, acc
# Define a classifier
def QClassifier(train_x, train_y, test_x, test_y, N, D, EPOCH, LR, BATCH, seed=0):
"""
Quantum binary classifier
"""
train_y = paddle.to_tensor(train_y, dtype="int64")
test_y = paddle.to_tensor(test_y, dtype="int64")
N_train, in_dim = train_x.shape
# Initialize the neural network
paddle.seed(0)
net = Net(n=N, depth=D)
# Generally speaking, we use Adam optimizer to obtain relatively good convergence,
# You can change it to SGD or RMS prop.
opt = paddle.optimizer.Adam(learning_rate=LR, parameters=net.parameters())
# Optimization loop
for ep in range(EPOCH):
for itr in range(N_train // BATCH):
input_state = train_x[itr * BATCH:(itr + 1) * BATCH]
input_state = reshape(input_state, [-1, 1, 2 ** N])
label = train_y[itr * BATCH:(itr + 1) * BATCH]
test_input_state = reshape(test_x, [-1, 1, 2 ** N])
# Forward propagation to calculate loss and accuracy
train_loss, train_acc = net(state_in=input_state, label=label)
if itr % 3 == 0:
# Compute test accuracy and loss
loss_useless, test_acc = net(state_in=test_input_state, label=test_y)
print("epoch:", ep, "iter:", itr,
"train loss: %.4f" % train_loss.numpy(),
"train acc: %.4f" % train_acc,
"test acc: %.4f" % test_acc)
# Use back propagation to minimize the loss function
train_loss.backward()
opt.minimize(train_loss)
opt.clear_grad()
# Compute test accuracy and loss
_, test_acc = net(state_in=test_input_state, label=test_y)
return test_acc.numpy()
time_start = time.time()
acc_list = []
for i in range(5):
print('***************************** qubit num : %s *****************************'%qubit_num_list[i])
train_x, train_y = train_data[i]
test_x, test_y = test_data[i]
acc = QClassifier(
train_x, # training data x
train_y, # training data label
test_x, # test data x
test_y, # test data label
N=qubit_num_list[i], # Number of qubits
D=qubit_num_list[i] + 2, # Circuit depth
EPOCH=5, # Number of training epochs
LR=0.05, # Learning rate
BATCH=200, # Batch size
seed=0
)
acc_list.append(acc)
time_span = time.time() - time_start
print('time used:', time_span, 's')
***************************** qubit num : 8 ***************************** epoch: 0 iter: 0 train loss: 0.6913 train acc: 0.5200 test acc: 0.4250 epoch: 0 iter: 3 train loss: 0.6836 train acc: 0.6500 test acc: 0.5200 epoch: 1 iter: 0 train loss: 0.6759 train acc: 0.6850 test acc: 0.5550 epoch: 1 iter: 3 train loss: 0.6709 train acc: 0.6950 test acc: 0.5650 epoch: 2 iter: 0 train loss: 0.6651 train acc: 0.6650 test acc: 0.5700 epoch: 2 iter: 3 train loss: 0.6621 train acc: 0.7050 test acc: 0.6050 epoch: 3 iter: 0 train loss: 0.6589 train acc: 0.6900 test acc: 0.6000 epoch: 3 iter: 3 train loss: 0.6597 train acc: 0.7050 test acc: 0.6250 epoch: 4 iter: 0 train loss: 0.6563 train acc: 0.7150 test acc: 0.6550 epoch: 4 iter: 3 train loss: 0.6566 train acc: 0.7250 test acc: 0.6700 ***************************** qubit num : 6 ***************************** epoch: 0 iter: 0 train loss: 0.6966 train acc: 0.4900 test acc: 0.5250 epoch: 0 iter: 3 train loss: 0.6938 train acc: 0.4850 test acc: 0.5450 epoch: 1 iter: 0 train loss: 0.6884 train acc: 0.5350 test acc: 0.5450 epoch: 1 iter: 3 train loss: 0.6862 train acc: 0.5400 test acc: 0.5700 epoch: 2 iter: 0 train loss: 0.6775 train acc: 0.5750 test acc: 0.5850 epoch: 2 iter: 3 train loss: 0.6744 train acc: 0.6100 test acc: 0.6000 epoch: 3 iter: 0 train loss: 0.6642 train acc: 0.6350 test acc: 0.5950 epoch: 3 iter: 3 train loss: 0.6615 train acc: 0.6450 test acc: 0.6200 epoch: 4 iter: 0 train loss: 0.6526 train acc: 0.6900 test acc: 0.6300 epoch: 4 iter: 3 train loss: 0.6560 train acc: 0.6250 test acc: 0.6350 ***************************** qubit num : 4 ***************************** epoch: 0 iter: 0 train loss: 0.7081 train acc: 0.4650 test acc: 0.5350 epoch: 0 iter: 3 train loss: 0.6994 train acc: 0.4950 test acc: 0.5900 epoch: 1 iter: 0 train loss: 0.6902 train acc: 0.5450 test acc: 0.5750 epoch: 1 iter: 3 train loss: 0.6942 train acc: 0.5150 test acc: 0.5800 epoch: 2 iter: 0 train loss: 0.6869 train acc: 0.6100 test acc: 0.5850 epoch: 2 iter: 3 train loss: 0.6923 train acc: 0.5150 test acc: 0.6000 epoch: 3 iter: 0 train loss: 0.6825 train acc: 0.5700 test acc: 0.6050 epoch: 3 iter: 3 train loss: 0.6917 train acc: 0.5200 test acc: 0.5950 epoch: 4 iter: 0 train loss: 0.6776 train acc: 0.5850 test acc: 0.5800 epoch: 4 iter: 3 train loss: 0.6901 train acc: 0.5450 test acc: 0.6050 ***************************** qubit num : 3 ***************************** epoch: 0 iter: 0 train loss: 0.7104 train acc: 0.4550 test acc: 0.5000 epoch: 0 iter: 3 train loss: 0.6931 train acc: 0.4950 test acc: 0.4900 epoch: 1 iter: 0 train loss: 0.6928 train acc: 0.4600 test acc: 0.4700 epoch: 1 iter: 3 train loss: 0.6968 train acc: 0.4800 test acc: 0.4800 epoch: 2 iter: 0 train loss: 0.6964 train acc: 0.5100 test acc: 0.4750 epoch: 2 iter: 3 train loss: 0.7004 train acc: 0.5150 test acc: 0.4600 epoch: 3 iter: 0 train loss: 0.6961 train acc: 0.5050 test acc: 0.4800 epoch: 3 iter: 3 train loss: 0.6957 train acc: 0.5300 test acc: 0.4850 epoch: 4 iter: 0 train loss: 0.6938 train acc: 0.5250 test acc: 0.5150 epoch: 4 iter: 3 train loss: 0.6919 train acc: 0.5150 test acc: 0.5250 ***************************** qubit num : 2 ***************************** epoch: 0 iter: 0 train loss: 0.7031 train acc: 0.5450 test acc: 0.4800 epoch: 0 iter: 3 train loss: 0.6960 train acc: 0.5350 test acc: 0.4550 epoch: 1 iter: 0 train loss: 0.6932 train acc: 0.5100 test acc: 0.5100 epoch: 1 iter: 3 train loss: 0.6930 train acc: 0.5250 test acc: 0.5200 epoch: 2 iter: 0 train loss: 0.6930 train acc: 0.5150 test acc: 0.4750 epoch: 2 iter: 3 train loss: 0.6933 train acc: 0.5050 test acc: 0.4600 epoch: 3 iter: 0 train loss: 0.6925 train acc: 0.5400 test acc: 0.4600 epoch: 3 iter: 3 train loss: 0.6909 train acc: 0.5350 test acc: 0.4700 epoch: 4 iter: 0 train loss: 0.6939 train acc: 0.5450 test acc: 0.4750 epoch: 4 iter: 3 train loss: 0.6853 train acc: 0.5600 test acc: 0.4750 time used: 184.6011986732483 s
The Petz-Rényi divergence of the average quantum state and the maximum mixed state¶
fig = plt.figure(1)
ax = axes([0.15, 0.15, 0.8, 0.8])
def average_encode_state(train_x):
d1, d2 = train_x.shape
density_matrices = np.reshape(train_x, [d1, d2, 1]) @ np.reshape(np.conj(train_x), [d1, 1, d2])
return np.mean(density_matrices, axis=0)
depth_list = [2, 3, 4, 6, 8]
Q_2Renyi_D3_list = []
Q_2Renyi_D6_list = []
for i,q in enumerate(qubit_num_list):
train_x, train_y = train_data[i]
train_x = train_x.numpy()
train_x0 = train_x[train_y == 0]
train_x1 = train_x[train_y == 1]
average_state0 = average_encode_state(train_x0.real)
average_state1 = average_encode_state(train_x1.real)
# print(average_state)
Q_2Renyi_D3 = np.log2(np.trace(average_state0 @ average_state0) * 2 ** q)
Q_2Renyi_D6 = np.log2(np.trace(average_state1 @ average_state1) * 2 ** q)
# bound = np.sum(np.sqrt(S0)) ** 2 / 2 ** num_qubits
Q_2Renyi_D3_list.append(Q_2Renyi_D3)
Q_2Renyi_D6_list.append(Q_2Renyi_D6)
print(Q_2Renyi_D3_list)
print(Q_2Renyi_D6_list)
func3, = ax.plot(depth_list, Q_2Renyi_D3_list, linewidth=1.5,
marker="<",
linestyle=":",
color="r"
)
func6, = ax.plot(depth_list, Q_2Renyi_D6_list, linewidth=1.5,
marker="o",
linestyle="-.",
color="g"
)
plt.xticks(fontsize=22)
plt.yticks(fontsize=22)
plt.xlabel("Depth", fontsize=22)
plt.ylabel(r"$D_2(\overline{\rho} || I/2^n)$", fontsize=22)
ax.semilogy()
ax.legend(handles=[func3, func6],
labels=["Digit 3", "Digit 6"],
loc="best",
fontsize=18)
ax.grid(axis="y")
plt.show()
[1.9842463368536747, 0.5256437464833253, 0.1964853652901484, 0.05162865627740749, 0.022790754263846934] [1.8628793706046225, 0.6064395532199834, 0.1529884926031612, 0.04173701231534178, 0.009023512622560221]
Investigating the effect on classification accuracy¶
print(acc_list)
fig = plt.figure(1)
ax = axes([0.15, 0.15, 0.8, 0.8])
func36_acc, = ax.plot(depth_list, acc_list, linewidth=1.5,
marker="*",
linestyle="--",
color="b"
)
plt.xticks(fontsize=22)
plt.yticks(fontsize=22)
plt.ylim(0.48, 0.75)
plt.xlabel("Depth", fontsize=22)
plt.ylabel(r"Test Accuracy", fontsize=22)
ax.legend(handles=[func36_acc,],
labels=["classifying 3 and 6"],
loc="best", fontsize=22)
ax.grid(axis="y")
plt.show()
[array([0.675], dtype=float32), array([0.61], dtype=float32), array([0.585], dtype=float32), array([0.535], dtype=float32), array([0.475], dtype=float32)]
Conclusion¶
According to the experimental results, the average quantum state of each category tends to the maximum mixed state at an exponential rate as the data encoding circuit deepens. As a result, the final quantum neural network's classification accuracy decreases. With the help of the literature [5], we have come to understand some of the limitations of angle coding. It is also acknowledged that designing a data coding strategy capable of solving real-world problems (often with high dimensionality of data features) is both urgent and difficult.
References¶
[1] Schuld, M. "Quantum machine learning models are kernel methods." arXiv preprint arXiv:2101.11020.(2021)
[2] Lloyd, Seth, et al. "Quantum embeddings for machine learning." arXiv preprint arXiv:2001.03622 (2020).
[3] Caro, Matthias C., et al. "Encoding-dependent generalization bounds for parametrized quantum circuits." Quantum 5 (2021): 582.
[4] Leonardo Banchi, et al. "Generalization in quantum machine learning: A quantum information standpoint." PRX Quantum 2.4 (2021): 040321.
[5] Li, Guangxi, et al. "Concentration of Data Encoding in Parameterized Quantum Circuits." arXiv preprint arXiv:2206.08273 (2022).