Quantum Autoencoder¶

Copyright (c) 2021 Institute for Quantum Computing, Baidu Inc. All Rights Reserved.

Overview¶

This tutorial will show how to train a quantum autoencoder to compress and reconstruct a given quantum state (mixed state) [1].

Theory¶

The form of the quantum autoencoder is very similar to the classical autoencoder, which is composed of an encoder $E$ and a decoder $D$. For the input quantum state $\rho_{in}$ of the $N$ qubit system (here we use the density operator representation of quantum mechanics to describe the mixed state), first use the encoder $E = U(\theta)$ to encode information into some of the qubits in the system. This part of qubits is denoted by system $A$. After measuring and discarding the remaining qubits (this part is denoted by system $B$), we get the compressed quantum state $\rho_{encode}$! The dimension of the compressed quantum state is the same as the dimension of the quantum system $A$. Suppose we need $N_A$ qubits to describe the system $A$, then the dimension of the encoded quantum state $\rho_{encode}$ is $2^{N_A}\times 2^{N_A}$. Note that the mathematical operation corresponding to the measure-and-discard operation in this step is partial trace. The reader can intuitively treat it as the inverse operation of the tensor product $\otimes$.

Let us look at a specific example. Given a quantum state $\rho_A$ of $N_A$ qubits and another quantum state $\rho_B$ of $N_B$ qubits, the quantum state of the entire quantum system composed of subsystems $A$ and $B$ is $\rho_{AB} = \rho_A \otimes \rho_B$, which is a state of $N = N_A + N_B$ qubits. Now we let the entire quantum system evolve under the action of the unitary matrix $U$ for some time to get a new quantum state $\tilde{\rho_{AB}} = U\rho_{AB}U^\dagger$. So if we only want to get the new quantum state $\tilde{\rho_A}$ of quantum subsystem A at this time, what should we do? We simply measure the quantum subsystem $B$ and then discard it. This step of the operation is completed by partial trace $\tilde{\rho_A} = \text{Tr}_B (\tilde{\rho_{AB}})$. With Paddle Quantum, we can call the built-in function partial_trace(rho_AB, 2**N_A, 2**N_B, 2) to complete this operation. Note: The last parameter is 2, which means that we want to discard quantum system $B$.

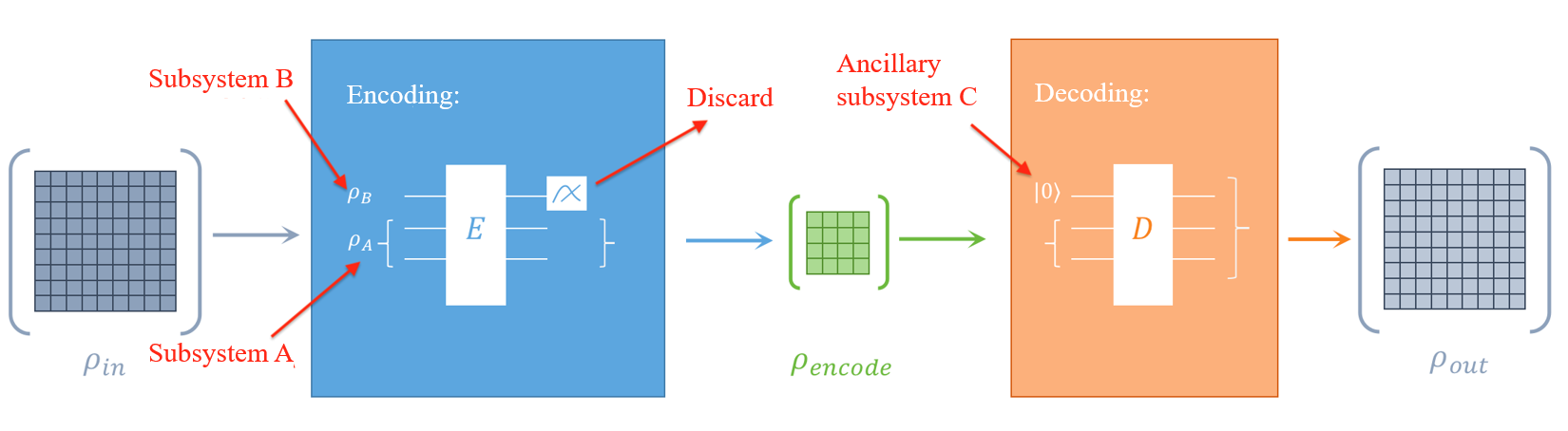
QA-fig-encoder_pipeline

After discussing the encoding process, let us take a look at how decoding is done. To decode the quantum state $\rho_{encode}$, we need to introduce an ancillary system $C$ with the same dimension as the system $B$ and take its initial state as the $|0\dots0\rangle$ state. Then use the decoder $D = U^\dagger(\theta)$ to act on the entire quantum system $A+C$ to decode the compressed information in system A. We hope that the final quantum state $\rho_{out}$ and $\rho_{in}$ are as similar as possible and use Uhlmann-Josza fidelity $F$ to measure the similarity between them.

$$ F(\rho_{in}, \rho_{out}) = \left(\operatorname{tr} \sqrt{\sqrt{\rho_{in}} \rho_{out} \sqrt{\rho_{in}}} \right)^{2}. \tag{1} $$

Finally, by optimizing the encoder's parameters, we can improve the fidelity of $\rho_{in}$ and $\rho_{out}$ as much as possible.

Paddle Quantum Implementation¶

Next, we will use a simple example to show the workflow of the quantum autoencoder. Here we first import the necessary packages.

In [1]:
from IPython.core.display import HTML
display(HTML("<style>pre { white-space: pre !important; }</style>"))
In [2]:
import numpy as np
import paddle
import paddle_quantum as pq
from paddle_quantum.ansatz.circuit import Circuit
from paddle_quantum.qinfo import state_fidelity, partial_trace
from paddle_quantum.linalg import dagger, haar_unitary
from paddle_quantum.state import State

Generating the initial state¶

Let us consider the quantum state $\rho_{in}$ of $N = 3$ qubits. We first encode the information into the two qubits below (system $A$) through the encoder then measure and discard the first qubit (system $B$). Secondly, we introduce another qubit (the new reference system $C$) in state $|0\rangle$ to replace the discarded qubit $B$. Finally, through the decoder, the compressed information in A is restored to $\rho_{out}$. Here, we assume that the initial state is a mixed state and the spectrum of $\rho_{in}$ is $\lambda_i \in \{0.4, 0.2, 0.2, 0.1, 0.1, 0, 0, 0\}$, and then generate the initial state $\rho_{in}$ by applying a random unitary transformation.

In [3]:
N_A = 2                          # Number of qubits in system A
N_B = 1                          # Number of qubits in system B
N = N_A + N_B                    # Total number of qubits
SEED = 15                        # Set random seed
complex_dtype = 'complex128'
paddle.seed(SEED)
pq.set_dtype(complex_dtype)        # set data type
pq.set_backend('density_matrix')

V = haar_unitary(N).numpy()                              # Generate a random unitary matrix
D = np.diag([0.4, 0.2, 0.2, 0.1, 0.1, 0, 0, 0])          # Set the spectrum of the target state rho
rho_in = State(V @ D @ dagger(V))     # Generate input state rho_in
rho_C = State(np.diag([1, 0]))     # Generate ancilla state rho_C

Building a quantum neural network¶

Here, we use quantum neural networks (QNN) as encoders and decoders. Suppose system A has $N_A$ qubits, both system $B$ and $C$ have $N_B$ qubits, and the depth of the QNN is $D$. Encoder $E$ acts on the total system composed of systems A and B, and decoder $D$ acts on the total system composed of $A$ and $C$. In this example, $N_{A} = 2$ and $N_{B} = 1$.

In [4]:
# Set circuit depth
cir_depth = 6

# Use Circuit class to build the encoder E
cir_Encoder = Circuit(N)
for _ in range(cir_depth):
    cir_Encoder.ry('full')
    cir_Encoder.rz('full')
    cir_Encoder.cnot('cycle')
print("The initialized circuit:") 
print(cir_Encoder)

The initialized circuit:
--Ry(2.974)----Rz(3.296)----*---------x----Ry(4.201)----Rz(4.559)----*---------x----Ry(5.254)----Rz(4.834)----*---------x----Ry(3.263)----Rz(1.664)----*---------x----Ry(5.240)----Rz(1.166)----*---------x----Ry(5.038)----Rz(0.564)----*---------x--
                            |         |                              |         |                              |         |                              |         |                              |         |                              |         |  
--Ry(2.407)----Rz(3.514)----x----*----|----Ry(6.279)----Rz(4.675)----x----*----|----Ry(4.986)----Rz(5.080)----x----*----|----Ry(2.845)----Rz(2.662)----x----*----|----Ry(0.015)----Rz(0.052)----x----*----|----Ry(4.341)----Rz(5.329)----x----*----|--
                                 |    |                                   |    |                                   |    |                                   |    |                                   |    |                                   |    |  
--Ry(3.866)----Rz(3.272)---------x----*----Ry(2.219)----Rz(2.298)---------x----*----Ry(6.060)----Rz(0.431)---------x----*----Ry(3.197)----Rz(1.673)---------x----*----Ry(2.324)----Rz(0.037)---------x----*----Ry(4.892)----Rz(1.856)---------x----*--

Configuring the training model: loss function¶

Here, we define the loss function to be

$$ Loss = 1-\langle 0...0|\rho_{trash}|0...0\rangle, \tag{2} $$

where $\rho_{trash}$ is the quantum state of the system $B$ discarded after encoding. Then we train the QNN through PaddlePaddle to minimize the loss function. If the loss function reaches 0, the input state and output state will be exactly the same state. This means that we have achieved compression and decompression perfectly, in which case the fidelity of the initial and final states is $F(\rho_{in}, \rho_{out}) = 1$.

In [6]:
# Set hyper-parameters
LR = 0.2       # Set the learning rate
ITR = 100      # Set the number of iterations

class NET(paddle.nn.Layer):
    def __init__(self, cir, rho_in, rho_C, dtype='float32'):
        super(NET, self).__init__()
        # load the circuit of the encoder E
        self.cir = cir
        # load the input state rho_in and the ancilla state rho_C
        self.rho_in = rho_in.data
        self.rho_C = rho_C.data
        # set trainable parameters
        self.theta = cir.parameters()
    
    # Define loss function and forward propagation mechanism
    def forward(self):
    
        # Generate the matrices of the encoder E and decoder D
        E = self.cir.unitary_matrix()
        E_dagger = dagger(E)
        D = E_dagger
        D_dagger = E

        # Encode the quantum state rho_in
        rho_BA = E @ self.rho_in @ E_dagger
        
        # Take partial_trace() to get rho_encode and rho_trash
        rho_encode = partial_trace(rho_BA, 2 ** N_B, 2 ** N_A, 1)
        rho_trash = partial_trace(rho_BA, 2 ** N_B, 2 ** N_A, 2)

        # Decode and get the quantum state rho_out
        rho_CA = paddle.kron(self.rho_C, rho_encode)
        rho_out = D @ rho_CA @ D_dagger
        
        # Calculate the loss function with rho_trash
        zero_Hamiltonian = paddle.to_tensor(np.diag([1, 0]).astype(complex_dtype))
        loss = 1 - paddle.real(paddle.trace(zero_Hamiltonian @ rho_trash))

        return loss, rho_out

# Generate network
net = NET(cir_Encoder, rho_in, rho_C)
# Generally speaking, we use Adam optimizer to get relatively good convergence
# Of course, it can be changed to SGD or RMS prop
opt = paddle.optimizer.Adam(learning_rate=LR, parameters=net.parameters())

# Optimization loops
for itr in range(1, ITR + 1):
    # Forward propagation for calculating loss function
    loss, rho_out = net()
    # Use back propagation to minimize the loss function
    loss.backward()
    opt.minimize(loss)
    opt.clear_grad()
    # Calculate and print fidelity
    fid = state_fidelity(rho_in, rho_out)
    if itr % 10 == 0:
        print('iter:', itr, 'loss:', '%.4f' % loss, 'fid:', '%.4f' % np.square(fid.item()))
    if itr == ITR:
        print("\nThe trained circuit:") 
        print(cir_Encoder)

iter: 10 loss: 0.1285 fid: 0.8609
iter: 20 loss: 0.1090 fid: 0.8800
iter: 30 loss: 0.1040 fid: 0.8877
iter: 40 loss: 0.1017 fid: 0.8899
iter: 50 loss: 0.1007 fid: 0.8913
iter: 60 loss: 0.1002 fid: 0.8923
iter: 70 loss: 0.1001 fid: 0.8925
iter: 80 loss: 0.1000 fid: 0.8925
iter: 90 loss: 0.1000 fid: 0.8925
iter: 100 loss: 0.1000 fid: 0.8926

The trained circuit:
--Ry(2.426)----Rz(3.029)----*---------x----Ry(4.490)----Rz(4.618)----*---------x----Ry(5.908)----Rz(4.413)----*---------x----Ry(1.273)----Rz(0.885)----*---------x----Ry(6.689)----Rz(1.169)----*---------x----Ry(5.038)----Rz(0.564)----*---------x--
                            |         |                              |         |                              |         |                              |         |                              |         |                              |         |  
--Ry(1.004)----Rz(3.807)----x----*----|----Ry(7.110)----Rz(5.279)----x----*----|----Ry(5.825)----Rz(6.107)----x----*----|----Ry(2.676)----Rz(2.543)----x----*----|----Ry(-1.62)----Rz(-1.07)----x----*----|----Ry(5.135)----Rz(5.329)----x----*----|--
                                 |    |                                   |    |                                   |    |                                   |    |                                   |    |                                   |    |  
--Ry(4.519)----Rz(1.909)---------x----*----Ry(3.341)----Rz(2.543)---------x----*----Ry(7.258)----Rz(-0.10)---------x----*----Ry(3.402)----Rz(2.748)---------x----*----Ry(3.975)----Rz(0.944)---------x----*----Ry(4.903)----Rz(1.856)---------x----*--

If the dimension of system A is denoted by $d_A$, it is easy to prove that the maximum fidelity can be achieved by quantum autoencoder is the sum of $d_A$ largest eigenvalues ​​of $\rho_{in}$. In our case $d_A = 4$ and the maximum fidelity is

$$ F_{\text{max}}(\rho_{in}, \rho_{out}) = \sum_{j=1}^{d_A} \lambda_j(\rho_{in})= 0.4 + 0.2 + 0.2 + 0.1 = 0.9. \tag{3} $$

After 100 iterations, the fidelity achieved by the quantum autoencoder we trained reaches above 0.89, which is very close to the optimal value.

References¶

[1] Romero, J., Olson, J. P. & Aspuru-Guzik, A. Quantum autoencoders for efficient compression of quantum data. Quantum Sci. Technol. 2, 045001 (2017).