Quantum Kernel Methods¶
Copyright (c) 2021 Institute for Quantum Computing, Baidu Inc. All Rights Reserved.
Introduction¶
One of the most important learning models for quantum machine learning applications in the noisy intermediate-scale quantum (NISQ) era is the parameterized quantum circuit. Although given its obvious analogy to classical neural networks, many refer to such quantum models as "quantum neural networks", it was shown that the mathematical form of such quantum machine learning models is actually much closer to kernel methods, a different kind of classical learning approach [1]. By combining classical kernel methods and the power of quantum models, quantum kernel methods can shed new light on how to approach a variety of machine learning problems, thus raising great interest in the field of quantum machine learning [2-7]. In this tutorial, we will introduce the basic ideas of quantum kernel methods and demonstrate how to classify data with two different quantum kernels.
Background¶
In classical machine learning, kernel methods' basic idea is to map a low-dimensional data vector into a potentially high-dimensional feature space via a feature map, thus giving us the possibility to use linear methods to analyze non-linear features in the original data. As shown in Fig. 1, by mapping linearly inseparable 1D data into a 2D feature space, the feature vectors of the original data become linearly separable.
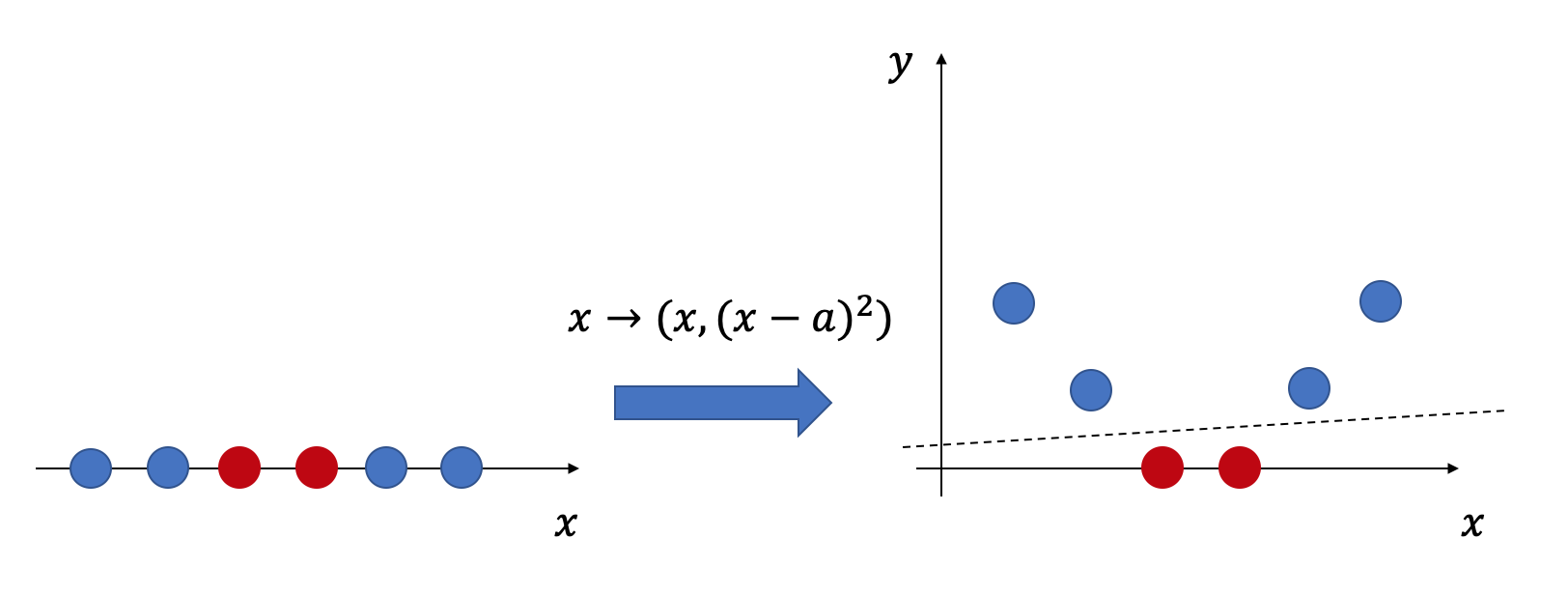
In practice, the feature space's dimensionality sometimes can be extremely large (even goes to infinity). So we do not wish to tackle these feature vectors directly. Another key idea in kernel methods is that we can implicitly analyze these feature vectors by only accessing their inner products in the feature space, which is noted as kernel functions :
with being the feature map. We note that in kernel methods, we do not need to express the feature map explicitly. Instead, we only need to compute the kernel function. This approach can introduce non-linearity into our models, giving us the ability to recognize intractable patterns in the original data space.
The arguably most famous application of kernel methods is the support vector machine (SVM), which solves linear classification problems. Take a 2-classification problem as an example: Given data set , with a hyperplane , a support vector machine can assign labels via the signs of the decision function, as:
But for linearly inseparable data, such linear classification schemes do not work. So again, as shown in Fig. 1, we can potentially find a better separation by mapping them into a feature space. For example, if we note the separating hyperplane in the feature space as , then the decision function becomes:
Furthermore, by duality, we can write the hyperplane as with Lagrangian multipliers [8]. Then, under the constraints and , we can compute the optimal , thus the optimal hyperplane by maximizing
Notice that in Eq. (4), we only need the inner products of feature vectors , which is the above mentioned kernel function. As a result, we are able to find the optimal separating hyperplane in the feature space with SVM by only accessing the feature space through the kernel function. Furthermore, we can compute the predicted label as follows:
Again, only kernel function is needed.
Given the idea of classical kernel methods, we can easily understand the essential idea of quantum kernel methods. First, consider a quantum feature space, where we map a classical data vector into a quantum state by a encoding circuit as follows:
There are many discussions about how to best design an encoding circuit. We refer to our data encoding tutorial for a more detailed explanation. The encoding can also be regarded as a quantum feature map from classical data space to the Hilbert space. Based on this idea, we define a quantum kernel function as the inner products of two quantum feature vectors in the Hilbert space, which is
which can be further formulated as
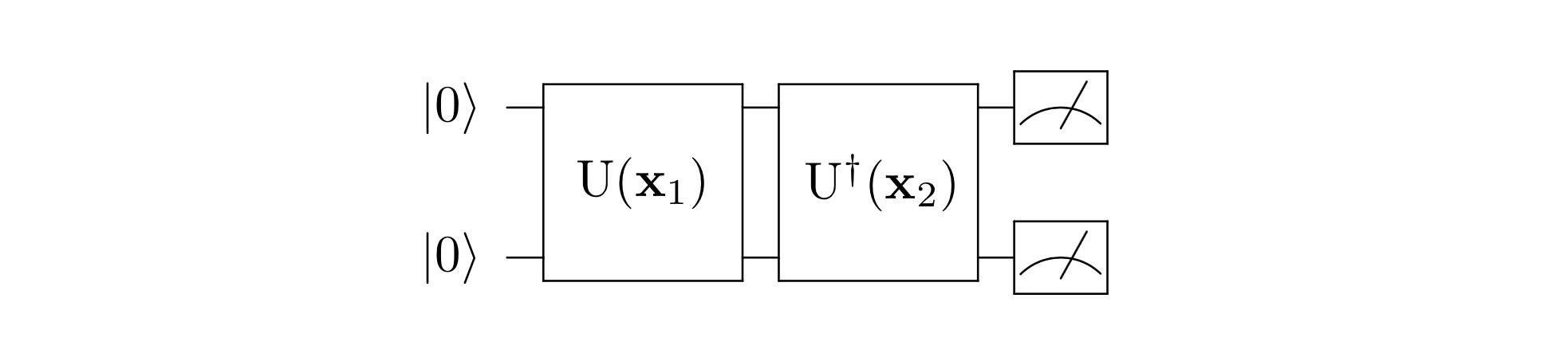
By running the quantum circuit as shown in Fig. 2, and measure the probability of observing at the output, we can estimate the quantum kernel function in Eq. (8). This way of constructing quantum kernels is also known as quantum kernel estimation (QKE). By replacing the classical kernel function in Eq. (4-5) with QKE, we can classify data in the quantum feature space with SVM. Given the potentially non-simulatable nature of such quantum kernels, there might exist a quantum advantage in recognizing classically intractable patterns. Such an advantage has been rigorously shown, with a constructed classically hard classification problem and a carefully designed quantum feature map [3].
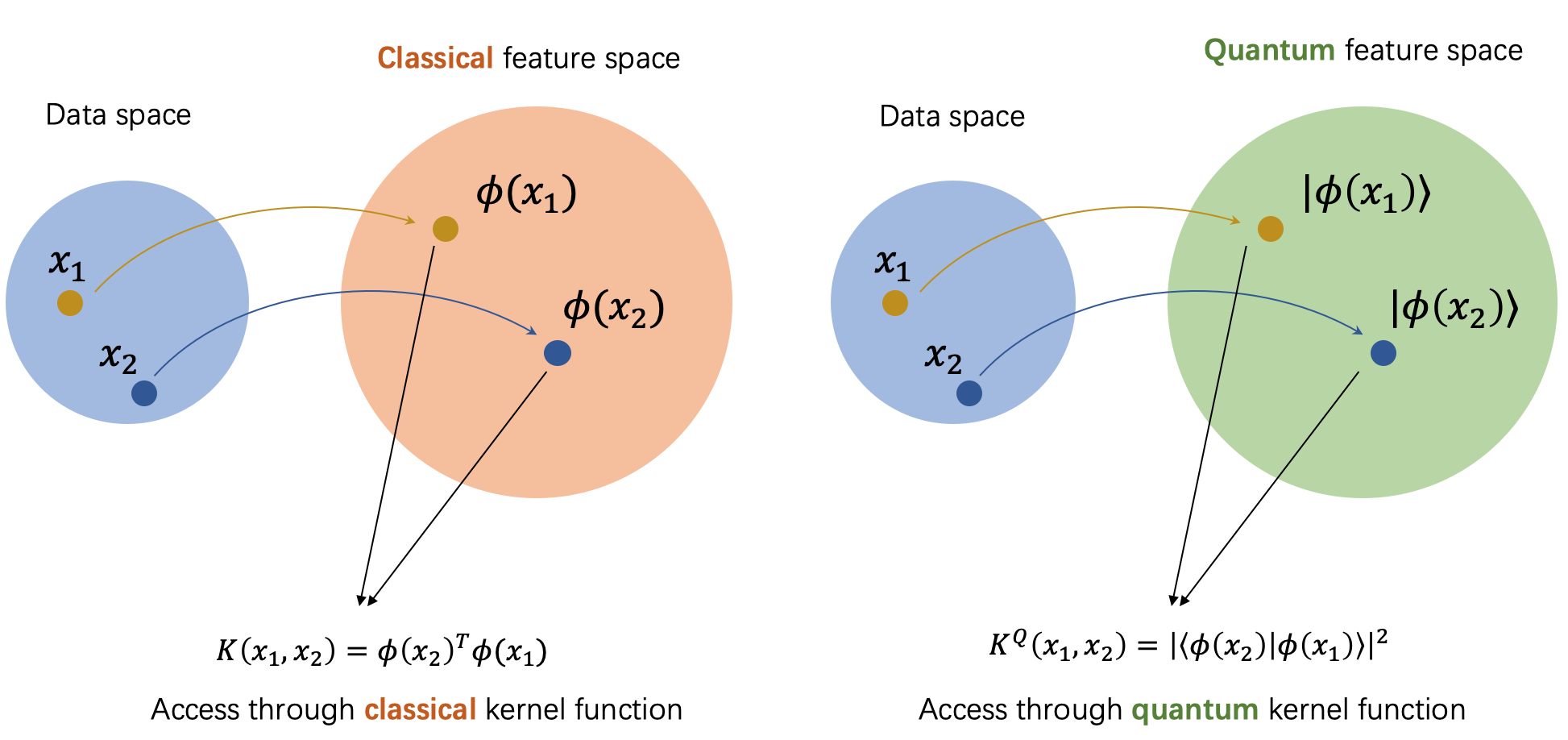
Connections between quantum machine learning and kernel methods¶
In quantum machine learning models, a quantum encoding circuit is often used to encode classical data into a quantum state
where is a parameterized quantum circuit depending on the data vector . Like we mentioned above, such quantum encoding circuit can be considered as a quantum feature map. Then, consider a "quantum neural network" is applied to the encoding state, in which the quantum circuit is composed of a set of parameterized gates with variational parameters. We have the final state as
where is the quantum neural network with parameters . Finally we perform a measurement on the final state as the output of our model, its expectation value can be computed as
Suppose we write the measurement in its operator form , then Eq. (11) can be further reformulated as
where . From Eq. (12), QNN together with a measurement can also be seen as a parameterized measurement operator, which is used to compute the inner product with the data encoding state in the Hilbert space, which is, the kernel function. This is why we mentioned in the introduction that the mathematical form of parameterized quantum circuits is closely related to kernel methods.
from IPython.display import clear_output
!pip install scikit-learn
clear_output()
In this tutorial, we will demonstrate how to classify data using a support vector machine with a kernel computed by Paddle Quantum.
import time
import matplotlib
import numpy as np
import paddle
from numpy import pi as PI
from matplotlib import pyplot as plt
from paddle import matmul, transpose
from paddle_quantum.ansatz import Circuit
from paddle_quantum.gate import IQPEncoding
import paddle_quantum
import sklearn
from sklearn import svm
from sklearn.datasets import fetch_openml, make_moons, make_circles
from sklearn.model_selection import train_test_split
from IPython.display import clear_output
from tqdm import tqdm
For the training and testing set, we generate some 2D circle data that has 2 classes.
# Generate data set
X_train, y_train = make_circles(10, noise=0.05, factor=0.2, random_state=0)
X_test, y_test = make_circles(10, noise=0.05, factor=0.2, random_state=1024)
# Visualize respectively the training and testing set
fig, ax = plt.subplots(1, 2, figsize=[10, 4])
ax[0].scatter(X_train[:,0], X_train[:,1],
marker='o', c = matplotlib.cm.coolwarm(np.array(y_train, dtype=np.float32)))
ax[0].set_title('Train')
ax[1].set_title('Test')
ax[1].scatter(X_test[:,0], X_test[:,1], marker='v', c = matplotlib.cm.coolwarm(np.array(y_test, dtype=np.float32)))
print("Let's first see our training and testing set:")
Let's first see our training and testing set:
# Initialize the progress bar
bar_format_string = '{l_bar}{bar}|[{elapsed}<{remaining}, ' '{rate_fmt}{postfix}]'
pbar = tqdm(total=100, bar_format=bar_format_string)
pbar.close()
clear_output()
Now, let's see how to implement a quantum kernel with Paddle Quantum:
# Global variable for manual updates of the progress bar
N = 1
# The QKE circuit simulated by paddle quantum
def q_kernel_estimator(x1, x2):
# Transform data vectors into tensors
x1 = paddle.to_tensor(x1)
x2 = paddle.to_tensor(x2)
# Create the circuit
cir = paddle_quantum.ansatz.Sequential()
# Add the encoding circuit for the first data vector
cir.append(IQPEncoding(qubits_idx=[[0,1]], feature=x1))
init_state = paddle_quantum.state.zero_state(2)
state = cir[0](state=init_state)
# Add inverse of the encoding circuit for the second data vector
cir.append(IQPEncoding(qubits_idx=[[0,1]], feature=x2))
fin_state = cir[1](state=state,invert=True).data
# Update the progress bar
global N
pbar.update(100/N)
# Return the probability of measuring 0...0
return (fin_state[0].conj() * fin_state[0]).real().numpy()[0]
# Define a kernel matrix function, for which the input should be two list of vectors
# This is needed to customize the SVM kernel
def q_kernel_matrix(X1, X2):
return np.array([[q_kernel_estimator(x1, x2) for x2 in X2] for x1 in X1])
# Visualize the decision function, boundary, and margins of +- 0.2
def visualize_decision_bound(clf):
# Create a 10x10 mesh in the data plan
x_min, x_max = X_train[:,0].min(), X_train[:,0].max()
y_min, y_max = X_train[:,1].min(), X_train[:,1].max()
XX, YY = np.meshgrid(np.linspace(-1.2, 1.2, 10),
np.linspace(-1.2, 1.2, 10))
# Calculate the decision function value on the 10x10 mesh
Z = clf.decision_function(np.c_[XX.ravel(), YY.ravel()])
Z_qke = Z.reshape(XX.shape)
# visualize the decision function and boundary
clear_output()
plt.contourf(XX, YY, Z_qke ,vmin=-1., vmax=1., levels=20,
cmap=matplotlib.cm.coolwarm, alpha=1)
plt.scatter(X_train[:,0], X_train[:,1],
c = matplotlib.cm.coolwarm(np.array(y_train, dtype=np.float32)),
edgecolor='black')
plt.scatter(X_test[:,0], X_test[:,1], marker='v',
c = matplotlib.cm.coolwarm(np.array(y_test, dtype=np.float32)),
edgecolor='black')
plt.contour(XX, YY, Z_qke, colors=['k', 'k', 'k'], linestyles=['--', '-', '--'],
levels=[-.2, 0, .2])
# To make sure we didn't make any mistake, check if the kernel function satisfies K(x, x)=1
print('Check if K(x, x) = 1?',
bool(abs(q_kernel_estimator(np.array([1. ,1.]), np.array([1., 1.])) - 1) < 1e-6))
Check if K(x, x) = 1? True
Then, let's try to use a support vector machine with a quantum kernel (QKE-SVM) to classify our data:
# Create the progress bar and the total kernel evaluation number N needed for training and prediction
pbar = tqdm(total=100,
desc='Training and predicting with QKE-SVM',
bar_format=bar_format_string)
N = len(X_train) ** 2 + len(X_train) ** 2 + len(X_train) * len(X_test)
# Create a support vector machine with a quantum kernel
svm_qke = svm.SVC(kernel=q_kernel_matrix)
# Train the svm with training data
svm_qke.fit(X_train, y_train)
# See how the svm classifies the training and testing data
predict_svm_qke_train = svm_qke.predict(X_train)
predict_svm_qke_test = svm_qke.predict(X_test)
# Calculate the accuracy
accuracy_train = np.array(predict_svm_qke_train == y_train, dtype=int).sum()/len(y_train)
accuracy_test = np.array(predict_svm_qke_test == y_test, dtype=int).sum()/len(y_test)
# Visualize the result
pbar.close()
clear_output()
fig, ax = plt.subplots(1, 2, figsize=[10, 4])
ax[0].scatter(X_train[:,0], X_train[:,1], marker='o',
c = matplotlib.cm.coolwarm(np.array(predict_svm_qke_train, dtype=np.float32)))
ax[0].set_title('Prediction on training set, accuracy={:.2f}'.format(accuracy_train))
ax[1].scatter(X_test[:,0], X_test[:,1], marker='v',
c = matplotlib.cm.coolwarm(np.array(predict_svm_qke_test, dtype=np.float32)))
ax[1].set_title('Prediction on testing set, accuracy={:.2f}'.format(accuracy_test))
print("Let's see how the QKE-SVM performs on the training on both the training and testing data:")
Let's see how the QKE-SVM performs on the training on both the training and testing data:
We can also visualize the decision function, also the decision boundary with margins of :
# Create the progress bar and the total kernel evaluation number N needed for visualizing the decision function
pbar = tqdm(total=100,
desc='Calculating the decision function of QKE-SVM',
bar_format=bar_format_string)
N = 10 ** 2 * len(X_train)
# Visualize the decision function
visualize_decision_bound(svm_qke)
pbar.close()
Calculating the decision function of QKE-SVM: 100%|██████████████████████████████▉|[00:09<00:00, 10.96it/s]
We can see that the quantum kernel has the ability to learn non-linearity correctly. As a matter of fact, the performance of quantum kernel methods in classification depends on whether the quantum feature map can distinguish non-trivial patterns hidden in the data. Currently, people are still exploring how to design a good quantum kernel: First, we may try different designs of encoding circuits; Second, we can train the quantum feature map to improve its classification accuracy [5-6]; Finally, we can also try variants of the quantum kernels [7].
In the following part, we will introduce another special kind of quantum kernel - projected quantum kernel.
Projected quantum kernel¶
It was mentioned above that quantum kernel methods can potentially distinguish intractable patterns by mapping classical data vectors into a quantum feature space via a quantum feature map. However, as the quantum feature space - the Hilbert space's dimensionality grows exponentially with the number of qubits, nearly all quantum states will be perpendicular to each other when we have a large number of qubits. Then the kernel matrix will just become an identity matrix , and the kernel methods would fail. To avoid this problem caused by extra dimensionality, we first need to extract features from the Hilbert space and then construct the kernel function with these extracted features. Following this idea, a variant of quantum kernel - projected quantum kernel is proposed : By projecting the quantum feature vectors back into the classical space with a set of measurements, the dimensionality problem is mitigated [7]. Also, as the projection can preserve important features of the quantum feature space, the projected kernel can still gain a quantum advantage.
There are several kinds of projected quantum kernels, here we choose the most rudimentary one:
where is the reduce density matrix of qubits , a set of measurements on the reduce density matrix. Here we take and , which means using Pauli measurements to measure every single qubit at the output.
Let's first try to implement a projected quantum kernel circuit with Paddle Quantum:
# First we can create a circuit to calculate the feature map
def projected_q_feature_map(x):
# turn data into tensor
x = paddle.to_tensor(x)
# Update the progress bar
global N
pbar.update(100/N)
init_state = paddle_quantum.state.zero_state(2)
res = []
# Take a projected measurement, returning its expected value as a classical feature
for op_pauli in ['z0', 'z1', 'x0', 'x1', 'y0', 'y1']:
cir = paddle_quantum.ansatz.Sequential()
cir.append(IQPEncoding(qubits_idx=[[0, 1]], feature=x))
state = cir[0](init_state)
hamiltonian = paddle_quantum.Hamiltonian([[1.0, op_pauli]])
cir.append(paddle_quantum.loss.ExpecVal(hamiltonian))
res.append(cir[1](state).numpy()[0])
return res
# to compute the projected quantum kernel based on the feature vectors
def p_quantum_kernel_estimator(x1, x2):
# compute the feature vector of each data and return the kernel function value
p_feature_vector_1 = np.array(projected_q_feature_map(x1))
p_feature_vector_2 = np.array(projected_q_feature_map(x2))
return np.exp(-((p_feature_vector_1 - p_feature_vector_2) ** 2).sum())
# similarly, define the kernel matrix as required
def p_quantum_kernel_matrix(X1, X2):
return np.array([[p_quantum_kernel_estimator(x1, x2) for x2 in X2] for x1 in X1])
Then, we replace the quantum kernel in the support vector machine with a projected quantum kernel, and see how the projected kernel performs on this classification task:
# Set the progress bar and the total kernel evaluation number N needed for training and prediction
pbar = tqdm(total=100,
desc='Training and predicting with PQK-SVM',
bar_format=bar_format_string)
N = 2 * (len(X_train) ** 2 + len(X_train) ** 2 + len(X_train) * len(X_test))
# Create a support vector machine with a quantum kernel
svm_pqk = svm.SVC(kernel=p_quantum_kernel_matrix)
# Train the svm with training data
svm_pqk.fit(X_train, y_train)
# See how the svm classifies the training and testing data
predict_svm_pqk_train = svm_pqk.predict(X_train)
predict_svm_pqk_test = svm_pqk.predict(X_test)
# Calculate the accuracy
accuracy_train = np.array(predict_svm_pqk_train == y_train, dtype=int).sum()/len(y_train)
accuracy_test = np.array(predict_svm_pqk_test == y_test, dtype=int).sum()/len(y_test)
# Visualize the result
pbar.close()
clear_output()
fig, ax = plt.subplots(1, 2, figsize=[10, 4])
ax[0].scatter(X_train[:,0], X_train[:,1], marker='o',
c = matplotlib.cm.coolwarm(np.array(predict_svm_pqk_train, dtype=np.float32)))
ax[0].set_title('Prediction on training set, accuracy={:.2f}'.format(accuracy_train))
ax[1].scatter(X_test[:,0], X_test[:,1], marker='v',
c = matplotlib.cm.coolwarm(np.array(predict_svm_pqk_test, dtype=np.float32)))
ax[1].set_title('Prediction on testing set, accuracy={:.2f}'.format(accuracy_test))
print("Let's see how the PQK-SVM performs on the training on both the training and testing data:")
Let's see how the PQK-SVM performs on the training on both the training and testing data:
# Set the progress bar and the total kernel evaluation number N needed for visualizing the decision function
pbar = tqdm(total=100,
desc='Calculating the decision function for PQK-SVM',
bar_format=bar_format_string)
N = 2 * 10 ** 2 * len(X_train)
# Clear the progress bar and visualize the decision function
visualize_decision_bound(svm_pqk)
pbar.close()
Calculating the decision function for PQK-SVM: 100%|█████████████████████████████▉|[01:17<00:00, 1.29it/s]
Conclusion¶
In quantum machine learning, people hope the design learning models which can gain quantum advantage by exploring the nature of quantum mechanics' laws. Recently, many connections are made between these quantum models and kernel methods, one of the most important classical machine learning approaches. In comparison to considering a parameterized quantum circuit as a "quantum neural network", where we focus on the variational ansatz , the quantum kernel methods emphasize the importance of quantum feature map , which describes how the classical data vectors is mapped to the quantum states. This brings new perspectives to how we can design novel quantum machine learning algorithms. Therefore, we encourage readers to together explore the performance of various quantum kernel designs on different data sets.
References¶
[1] Schuld, Maria. "Supervised quantum machine learning models are kernel methods." arXiv preprint arXiv:2101.11020 (2021).
[2] Havlíček, Vojtěch, et al. "Supervised learning with quantum-enhanced feature spaces." Nature 567.7747 (2019): 209-212.
[3] Liu, Yunchao, Srinivasan Arunachalam, and Kristan Temme. "A rigorous and robust quantum speed-up in supervised machine learning." arXiv preprint arXiv:2010.02174 (2020).
[4] Schuld, Maria, and Nathan Killoran. "Quantum machine learning in feature Hilbert spaces." Phys. Rev. Lett. 122.4 (2019): 040504.
[5] Hubregtsen, Thomas, et al. "Training Quantum Embedding Kernels on Near-Term Quantum Computers." arXiv preprint arXiv:2105.02276(2021).
[6] Glick, Jennifer R., et al. "Covariant quantum kernels for data with group structure." arXiv preprint arXiv:2105.03406(2021).
[7] Huang, Hsin-Yuan, et al. "Power of data in quantum machine learning." arXiv preprint arXiv:2011.01938 (2020).
[8] Schölkopf, Bernhard, and Alexander J. Smola"Learning with kernels: support vector machines, regularization, optimization, and beyond." MIT Press(2002).