Variational Shadow Quantum Learning

Copyright (c) 2021 Institute for Quantum Computing, Baidu Inc. All Rights Reserved.

Overview

In this tutorial, we will discuss the workflow of Variational Shadow Quantum Learning (VSQL) [1] and accomplish a binary classification task using VSQL. VSQL is a hybird quantum-classical framework for supervised quantum learning, which utilizes parameterized quantum circuits and classical shadows. Unlike commonly used variational quantum algorithms, the VSQL method extracts "local" features from the subspace instead of the whole Hilbert space.

Background

We consider a $k$-label classification problem. The input is a set containing $N$ labeled data points $D=\left\{(\mathbf{x}^i, \mathbf{y}^i)\right\}_{i=1}^{N}$, where $\mathbf{x}^i\in\mathbb{R}^{m}$ is the data point and $\mathbf{y}^i$ is a one-hot vector with length $k$ indicating which category the corresponding data point belongs to. Representing the labels as one-hot vectors is a common choice within the machine learning community. For example, for $k=3$, $\mathbf{y}^{a}=[1, 0, 0]^\text{T}, \mathbf{y}^{b}=[0, 1, 0]^\text{T}$, and $\mathbf{y}^{c}=[0, 0, 1]^\text{T}$ indicate that the $a^{\text{th}}$, the $b^{\text{th}}$, and the $c^{\text{th}}$ data points belong to class 0, class 1, and class 2, respectively. The learning process aims to train a model $\mathcal{F}$ to predict the label of every data point as accurately as possible.

The realization of $\mathcal{F}$ in VSQL is a combination of parameterized local quantum circuits, known as shadow circuits, and a classical fully-connected neural network (FCNN). VSQL requires preprocessing to encode classical information into quantum states. After encoding the data, we convolutionally apply a parameterized local quantum circuit $U(\mathbf{\theta})$ to qubits in each encoded quantum state, where $\mathbf{\theta}$ is the vector of parameters in the circuit. Then, expectation values are obtained via measuring local observables on these qubits. After the measurement, there is an additional classical FCNN for postprocessing.

We can write the output of $\mathcal{F}$, which is obtained from VSQL, as $\tilde{\mathbf{y}}^i = \mathcal{F}(\mathbf{x}^i)$. Here $\tilde{\mathbf{y}}^i$ is a probability distribution, where $\tilde{y}^i_j$ is the probability of the $i^{\text{th}}$ data point belonging to the $j^{\text{th}}$ class. In order to predict the actual label, we calculate the cumulative distance between $\tilde{\mathbf{y}}^i$ and $\mathbf{y}^i$ as the loss function $\mathcal{L}$ to be optimized:

$$ \mathcal{L}(\mathbf{\theta}, \mathbf{W}, \mathbf{b}) = -\frac{1}{N}\sum\limits_{i=1}^{N}\sum\limits_{j=1}^{k}y^i_j\log{\tilde{y}^i_j}, \tag{1} $$

where $\mathbf{W}$ and $\mathbf{b}$ are the weights and the bias of the one layer FCNN. Note that this loss function is derived from cross-entropy [2].

Pipeline

Figure 1: Flow chart of VSQL

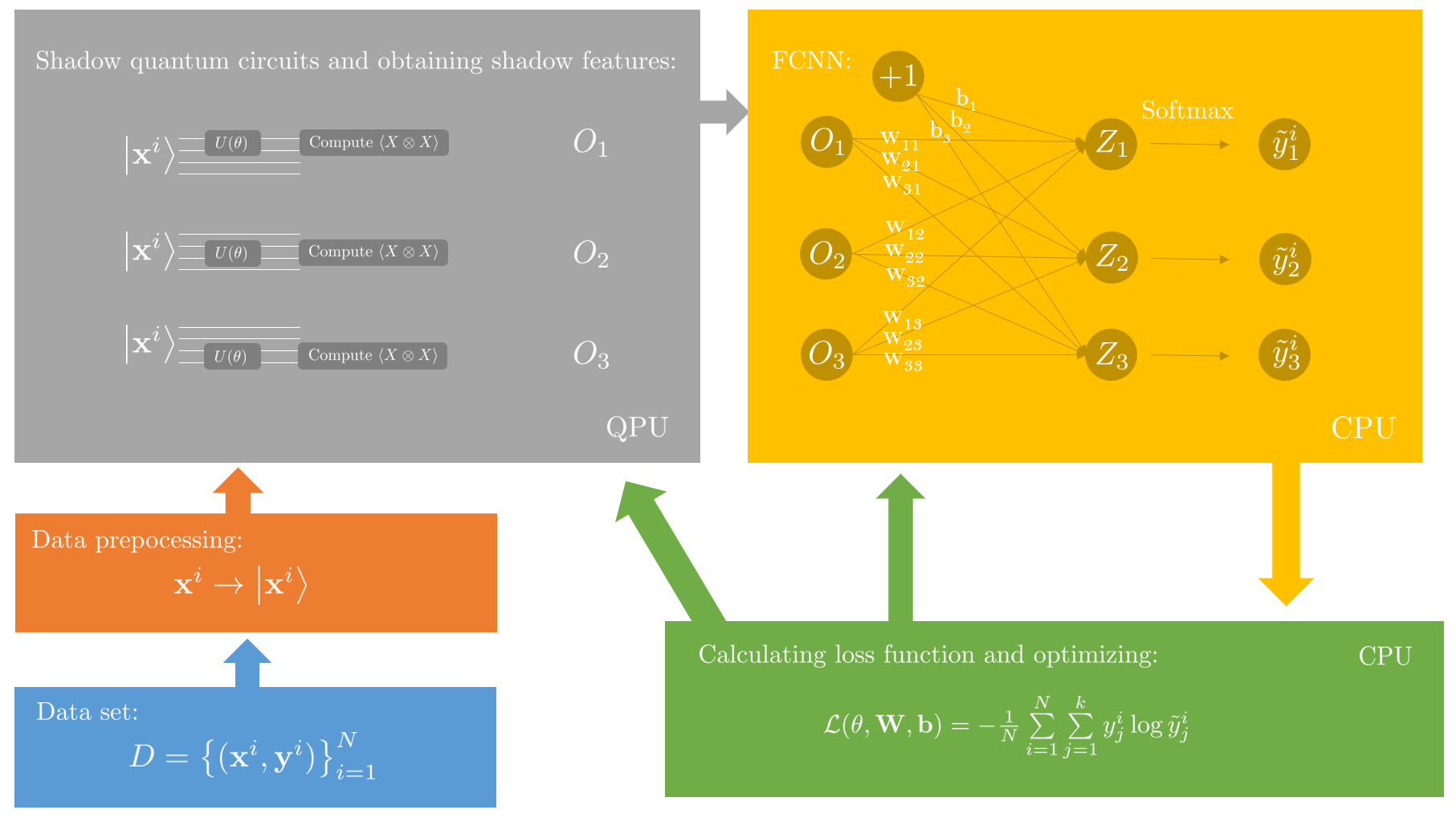
Here we give the whole pipeline to implement VSQL.

1. Encode a classical data point $\mathbf{x}^i$ into a quantum state $\left|\mathbf{x}^i\right>$.
2. Prepare a parameterized local quantum circuit $U(\mathbf{\theta})$ and initialize its parameters $\mathbf{\theta}$.
3. Apply $U(\mathbf{\theta})$ on the first few qubits. Then, obtain a shadow feature via measuring a local observable, for instance, $X\otimes X\cdots \otimes X$, on these qubits.
4. Sliding down $U(\mathbf{\theta})$ one qubit each time, repeat step 3 until the last qubit has been covered.
5. Feed all shadow features obtained from steps 3-4 to an FCNN and get the predicted label $\tilde{\mathbf{y}}^i$ through an activation function. For multi-label classification problems, we use the softmax activation function.
6. Repeat steps 3-5 until all data points in the data set have been processed. Then calculate the loss function $\mathcal{L}(\mathbf{\theta}, \mathbf{W}, \mathbf{b})$.
7. Adjust the parameters $\mathbf{\theta}$, $\mathbf{W}$, and $\mathbf{b}$ through optimization methods such as gradient descent to minimize the loss function. Then we get the optimized model $\mathcal{F}$.

Since VSQL only extracts local shadow features, it can be easily implemented on quantum devices with topological connectivity limits. Besides, since the $U(\mathbf{\theta})$ used in circuits are identical, the number of parameters involved is significantly smaller than other commonly used variational quantum classifiers.

Paddle Quantum Implementation

We will apply VSQL to classify handwritten digits taken from the MNIST dataset [3], a public benchmark dataset containing ten different classes labeled from '0' to '9'. Here, we consider a binary classification problem for the prupose of demonstration, in which only data labeled as '0' or '1' are used.

First, we import the required packages.

import time
import numpy as np
import paddle
import paddle.nn.functional as F
from paddle.vision.datasets import MNIST
import paddle_quantum
from paddle_quantum.ansatz import Circuit

Data preprocessing

Each image of a handwritten digit consists of $28\times 28$ grayscale pixels valued in $[0, 255]$. We first flatten the $28\times 28$ 2D matrix into a 1D vector $\mathbf{x}^i$, and use amplitude encoding to encode every $\mathbf{x}^i$ into a 10-qubit quantum state $\left|\mathbf{x}^i\right>$. To do amplitude encoding, we first normalize each vector and pad it with zeros at the end.

# Normalize the vector and do zero-padding
def norm_img(images):
    new_images = [np.pad(np.array(i).flatten(), (0, 240), constant_values=(0, 0)) for i in images]
    new_images = [paddle.to_tensor(i / np.linalg.norm(i), dtype='complex64') for i in new_images]

    return new_images

def data_loading(n_train=1000, n_test=100):
    # We use the MNIST provided by paddle
    train_dataset = MNIST(mode='train')
    test_dataset = MNIST(mode='test')
    # Select data points from category 0 and 1
    train_dataset = np.array([i for i in train_dataset if i[1][0] == 0 or i[1][0] == 1], dtype=object)
    test_dataset = np.array([i for i in test_dataset if i[1][0] == 0 or i[1][0] == 1], dtype=object)
    np.random.shuffle(train_dataset)
    np.random.shuffle(test_dataset)
    # Separate images and labels
    train_images = train_dataset[:, 0][:n_train]
    train_labels = train_dataset[:, 1][:n_train].astype('int64')
    test_images = test_dataset[:, 0][:n_test]
    test_labels = test_dataset[:, 1][:n_test].astype('int64')
    # Normalize data and pad them with zeros
    x_train = norm_img(train_images)
    x_test = norm_img(test_images)
    # Transform integer labels into one-hot vectors
    train_targets = np.array(train_labels).reshape(-1)
    y_train = paddle.to_tensor(np.eye(2)[train_targets])
    test_targets = np.array(test_labels).reshape(-1)
    y_test = paddle.to_tensor(np.eye(2)[test_targets])

    return x_train, y_train, x_test, y_test

Building the shadow circuit

Now, we are ready for the next step. Before diving into details of the circuit, we need to clarify several parameters:

• $n$: the number of qubits encoding each data point.
• $n_{qsc}$: the width of the quantum shadow circuit . We only apply $U(\mathbf{\theta})$ on consecutive $n_{qsc}$ qubits each time.
• $D$: the depth of the circuit, indicating the repeating times of a layer in $U(\mathbf{\theta})$.

Here, we give an example where $n = 4$ and $n_{qsc} = 2$.

We first apply $U(\mathbf{\theta})$ to the first two qubits and obtain the shadow feature $O_1$.

Figure 2: The first circuit

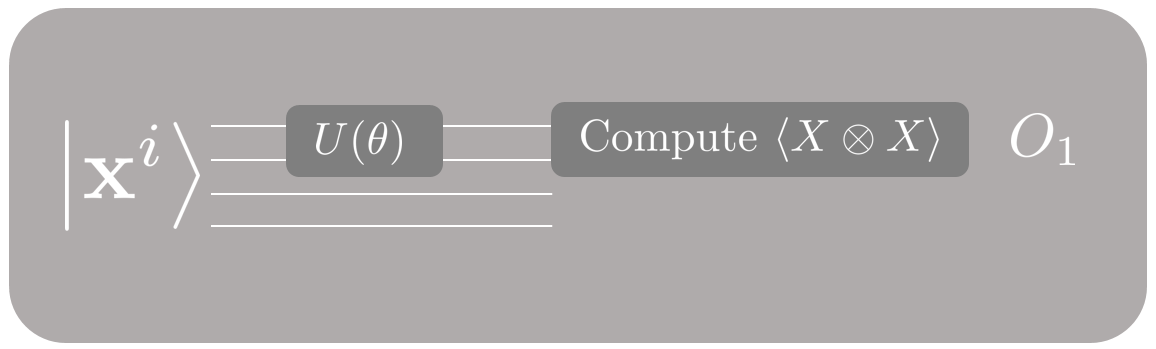
Then, we prepare a copy of the same input state $\left|\mathbf{x}^i\right>$, apply $U(\mathbf{\theta})$ to the two qubits in the middle, and obtain the shadow feature $O_2$.

Figure 3: The second circuit

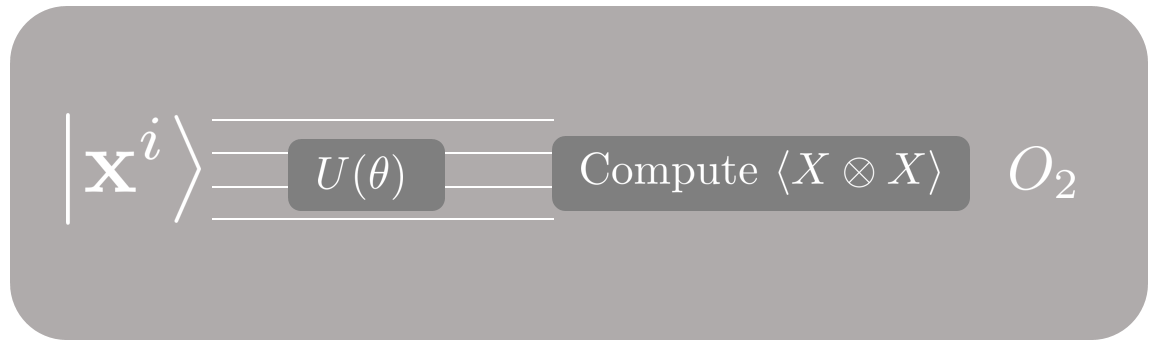
Finally, we prepare another copy of the same input state, apply $U(\mathbf{\theta})$ to the last two qubits, and obtain the shadow feature $O_3$. Now we are done with this data point!

Figure 4: The last circuit

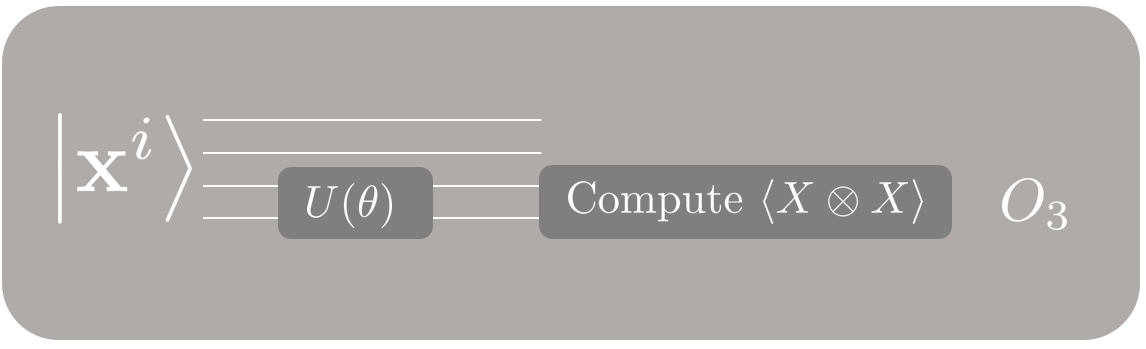
In general, we will need to repeat this process for $n - n_{qsc} + 1$ times for each data point. One thing to point out is that we only use one shadow circuit in the above example. When sliding the shadow circuit $U(\mathbf{\theta})$ through the $n$-qubit Hilbert space, the same parameters $\mathbf{\theta}$ are used. You can use more shadow circuits for complicated tasks, and different shadow circuits should have different parameters $\mathbf{\theta}$.

Below, we will use a 2-local shadow circuit, i.e., $n_{qsc}=2$ for the MNIST classification task, and the circuit's structure is shown in Figure 5.

Figure 5: The 2-local shadow circuit design

The circuit layer in the dashed box is repeated for $D$ times to increase the expressive power of the quantum circuit. The structure of the circuit is not unique. You can try to design your own circuit.

# Construct the shadow circuit U(theta)
def U_theta(n, n_qsc=2, depth=1):
    # Initialize the circuit
    cir = Circuit(n)
    # Add layers of rotation gates
    for i in range(n_qsc):
        cir.rx(qubits_idx=i)
        cir.ry(qubits_idx=i)
        cir.rx(qubits_idx=i)
    # Add D layers of the dashed box
    for repeat in range(1, depth + 1):
        for i in range(n_qsc - 1):
            cir.cnot([i, i + 1])
        cir.cnot([n_qsc - 1, 0])
        for i in range(n_qsc):
            cir.ry(qubits_idx=i)

    return cir

# Slide the circuit
def slide_circuit(cir, distance):
    for sublayer in cir.sublayers():
        qubits_idx = np.array(sublayer.qubits_idx)
        qubits_idx = qubits_idx + distance
        sublayer.qubits_idx = qubits_idx.tolist()

When $n_{qsc}$ is larger, the $n_{qsc}$-local shadow circuit can be constructed by extending this 2-local shadow circuit. Let's print a 4-local shadow circuit with $D=2$ to find out how it works.

N = 6
NQSC = 4
D = 2
cir = U_theta(N, n_qsc=NQSC, depth=D)
print(cir)

--Rx(2.461)----Ry(5.857)----Rx(1.809)----*--------------x----Ry(4.381)----*--------------x----Ry(1.523)--
                                         |              |                 |              |               
--Rx(3.861)----Ry(5.536)----Rx(3.228)----x----*---------|----Ry(1.633)----x----*---------|----Ry(2.853)--
                                              |         |                      |         |               
--Rx(3.690)----Ry(5.288)----Rx(2.211)---------x----*----|----Ry(0.397)---------x----*----|----Ry(6.159)--
                                                   |    |                           |    |               
--Rx(3.030)----Ry(5.486)----Rx(3.769)--------------x----*----Ry(1.769)--------------x----*----Ry(2.564)--
                                                                                                         
---------------------------------------------------------------------------------------------------------
                                                                                                         
---------------------------------------------------------------------------------------------------------
                                                                                                         

Shadow features

We've talked a lot about shadow features, but what is a shadow feature? It can be seen as a projection of a state from Hilbert space to classical space. There are various projections that can be used as a shadow feature. Here, we choose the expectation value of the Pauli $X\otimes X\otimes \cdots \otimes X$ observable on selected $n_{qsc}$ qubits as the shadow feature. In our previous example, $O_1 = \left<X\otimes X\right>$ on the first two qubits is the first shadow feature we extracted with the shadow circuit.

# Construct the observable for extracting shadow features
def observable(n_start, n_qsc=2):
    pauli_str = ','.join('x' + str(i) for i in range(n_start, n_start + n_qsc))
    hamiltonian = paddle_quantum.Hamiltonian([[1.0, pauli_str]])

    return hamiltonian

Classical postprocessing with FCNN

After obtaining all shadow features, we feed them into a classical FCNN. We use the softmax activation function so that the output from the FCNN will be a probability distribution. The $i^{\text{th}}$ element of the output is the probability of this data point belonging to the $i^{\text{th}}$ category, and we predict this data point belongs to the category with the highest probability. In order to predict the actual label, we calculate the cumulative distance between the predicted label and the actual label as the loss function to be optimized:

$$ \mathcal{L}(\mathbf{\theta}, \mathbf{W}, \mathbf{b}) = -\frac{1}{N}\sum\limits_{i=1}^{N}\sum\limits_{j=1}^{k}y^i_j\log{\tilde{y}^i_j}. \tag{2} $$

class Net(paddle.nn.Layer):
    def __init__(self,
                 n, # Number of qubits: n     
                 n_qsc, # Number of local qubits in a shadow
                 depth=1 # Circuit depth
                ):
        super(Net, self).__init__()
        self.n = n
        self.n_qsc = n_qsc
        self.depth = depth
        self.cir = U_theta(self.n, n_qsc=self.n_qsc, depth=self.depth)
        # FCNN, initialize the weights and the bias with a Gaussian distribution
        self.fc = paddle.nn.Linear(n - n_qsc + 1, 2,
                                   weight_attr=paddle.ParamAttr(initializer=paddle.nn.initializer.Normal()),
                                   bias_attr=paddle.ParamAttr(initializer=paddle.nn.initializer.Normal()))

    # Define forward propagation mechanism, and then calculate loss function and cross-validation accuracy
    def forward(self, batch_in, label):
        # Quantum part
        dim = len(batch_in)
        features = []
        for state in batch_in:
            _state = paddle_quantum.State(state)
            f_i = []
            for st in range(self.n - self.n_qsc + 1):
                ob = observable(st, n_qsc=self.n_qsc)
                # Slide the circuit to act on different qubits
                slide_circuit(self.cir, 1 if st != 0 else 0)
                expecval = paddle_quantum.loss.ExpecVal(ob)
                out_state = self.cir(_state)
                # Calculate the expectation value
                f_ij = expecval(out_state)
                f_i.append(f_ij)
            # Slide the circuit back to the initial position
            slide_circuit(self.cir, -st)
            f_i = paddle.concat(f_i)
            features.append(f_i)
        features = paddle.stack(features)
        # Classical part
        outputs = self.fc(features)
        outputs = F.log_softmax(outputs)
        # Calculate loss and accuracy
        loss = -paddle.mean(paddle.sum(outputs * label)) 
        is_correct = 0
        for i in range(dim):
            if paddle.argmax(label[i], axis=-1) == paddle.argmax(outputs[i], axis=-1):
                is_correct = is_correct + 1
        acc = is_correct / dim

        return loss, acc

def ShadowClassifier(N=4, n_qsc=2, D=1, EPOCH=4, LR=0.1, BATCH=1, N_train=1000, N_test=100):
    # Load data
    x_train, y_train, x_test, y_test = data_loading(n_train=N_train, n_test=N_test)
    # Initialize the neural network
    net = Net(N, n_qsc, depth=D)
    # Generally speaking, we use Adam optimizer to obtain relatively good convergence,
    # You can change it to SGD or RMS prop.
    opt = paddle.optimizer.Adam(learning_rate=LR, parameters=net.parameters())

    # Optimization loop
    for ep in range(EPOCH):
        for itr in range(N_train // BATCH):
            # Forward propagation to calculate loss and accuracy
            loss, batch_acc = net(x_train[itr * BATCH:(itr + 1) * BATCH],
                                  y_train[itr * BATCH:(itr + 1) * BATCH])
            # Use back propagation to minimize the loss function
            loss.backward()
            opt.minimize(loss)
            opt.clear_grad()
            # Evaluation
            if itr % 10 == 0:
                # Compute test accuracy and loss
                loss_useless, test_acc = net(x_test[0:N_test],
                                             y_test[0:N_test])
                # Print test results
                print("epoch:%3d" % ep, "  iter:%3d" % itr,
                      "  loss: %.4f" % loss.numpy(),
                      "  batch acc: %.4f" % batch_acc,
                      "  test acc: %.4f" % test_acc)

Let's take a look at the actual training process, which takes about eight minutes:

time_st = time.time()
ShadowClassifier(
    N=10,         # Number of qubits: n
    n_qsc=2,      # Number of local qubits in a shadow: n_qsc
    D=1,          # Circuit depth
    EPOCH=3,      # Number of training epochs
    LR=0.02,      # Learning rate
    BATCH=20,     # Batch size
    N_train=500,  # Number of training data
    N_test=100    # Number of test data
)
print("time used:", time.time() - time_st)

C:\Users\v_zhaoxuanqiang\AppData\Local\Temp\ipykernel_9684\2285585707.py:6: FutureWarning: The input object of type 'Image' is an array-like implementing one of the corresponding protocols (`__array__`, `__array_interface__` or `__array_struct__`); but not a sequence (or 0-D). In the future, this object will be coerced as if it was first converted using `np.array(obj)`. To retain the old behaviour, you have to either modify the type 'Image', or assign to an empty array created with `np.empty(correct_shape, dtype=object)`.
  train_dataset = np.array([i for i in train_dataset if i[1][0] == 0 or i[1][0] == 1], dtype=object)
C:\Users\v_zhaoxuanqiang\AppData\Local\Temp\ipykernel_9684\2285585707.py:7: FutureWarning: The input object of type 'Image' is an array-like implementing one of the corresponding protocols (`__array__`, `__array_interface__` or `__array_struct__`); but not a sequence (or 0-D). In the future, this object will be coerced as if it was first converted using `np.array(obj)`. To retain the old behaviour, you have to either modify the type 'Image', or assign to an empty array created with `np.empty(correct_shape, dtype=object)`.
  test_dataset = np.array([i for i in test_dataset if i[1][0] == 0 or i[1][0] == 1], dtype=object)

epoch:  0   iter:  0   loss: 15.8133   batch acc: 0.4500   test acc: 0.4700
epoch:  0   iter: 10   loss: 12.3796   batch acc: 0.7500   test acc: 0.8800
epoch:  0   iter: 20   loss: 11.3694   batch acc: 0.8500   test acc: 0.9600
epoch:  1   iter:  0   loss: 9.0114   batch acc: 0.9000   test acc: 0.9700
epoch:  1   iter: 10   loss: 8.0621   batch acc: 0.9500   test acc: 0.9700
epoch:  1   iter: 20   loss: 8.1941   batch acc: 0.9000   test acc: 0.9800
epoch:  2   iter:  0   loss: 6.5335   batch acc: 0.9000   test acc: 0.9900
epoch:  2   iter: 10   loss: 6.2066   batch acc: 0.9000   test acc: 0.9900
epoch:  2   iter: 20   loss: 6.6691   batch acc: 0.9000   test acc: 0.9900
time used: 499.0781090259552

Conclusion

VSQL is a hybrid quantum-classical algorithm based on classical shadows, which extracts local features in a convolution way. Combing parameterized circuit $U(\mathbf{\theta})$ with a classical FCNN, VSQL demonstrates a good performance in binary classification tasks. In the quantum classifier tutorial, we have introduced a commonly used classifier using a parameterized quantum circuit. In that framework, the parameterized circuit is applied to all qubits, and the optimization process searches through the whole Hilbert space to find the optimized $\mathbf{\theta}$. Unlike that method, in VSQL, the parameterized circuit $U(\mathbf{\theta})$ is only applied to a few selected qubits each time. The number of parameters of VSQL for $k$-label classification is the sum of parameters in $U(\mathbf{\theta})$ and parameters in FCNN, which is in total $n_{qsc}D + [(n-n_{qsc}+1)+1]k$. Compared to commonly used variational quantum classifiers that need $nD$ parameters in the parameterized quantum circuit, VSQL only has $n_{qsc}D$ parameters in the parameterized local quantum circuit. As a result, the amount of quantum resources (the number of quantum gates) required has been significantly reduced.

---

References

[1] Li, Guangxi, Zhixin Song, and Xin Wang. "VSQL: Variational Shadow Quantum Learning for Classification." Proceedings of the AAAI Conference on Artificial Intelligence. Vol. 35. No. 9. 2021.

[2] Goodfellow, Ian, et al. Deep learning. Vol. 1. No. 2. Cambridge: MIT press, 2016.

[3] LeCun, Yann. "The MNIST database of handwritten digits." http://yann.lecun.com/exdb/mnist/ (1998).