VAns: Variable Ansatz¶
Copyright (c) 2022 Institute for Quantum Computing, Baidu Inc. All Rights Reserved.
Overview¶
Variational Quantum Algorithms (VQA) are about to tune parameters of quantum circuits to minimize an objective function of interest. The commonly used VQAs, like Variational Quantum Eigensolvers (VQE) and Quantum Approximate Optimization Algorithm (QAOA), perform optimization using a user-defined ansatz with fixed structure. However, if the ansatz is too simple or shallow, the expressivity of the circuit will not be insufficient to get the optimal value for the objective function. On the other side, if the ansatz is overly complicated or long, we may encounter barren plateau effect, which impedes us from obtaining the global minimum value. Thus, a circuit structure design search algorithm will be helpful to find the appropriate circuit for a specific task.
In this tutorial, we will discuss a circuit architecture design search algorithm called Variable ansatz (VAns) [1]. Starting with an initial circuit, VAns keeps inserting and deleting gates during the optimization process in order to minimize the loss function as well as keep the circuit shallow. We will use this method to accomplish an adjusted version of VQE task and compare the resulting circuit with the original VQE circuit.
Pipeline¶
VAns consists of the following steps:
- Start with an initial circuit. Run the inner optimization, which is just the original VQE process, and get the optimal value.
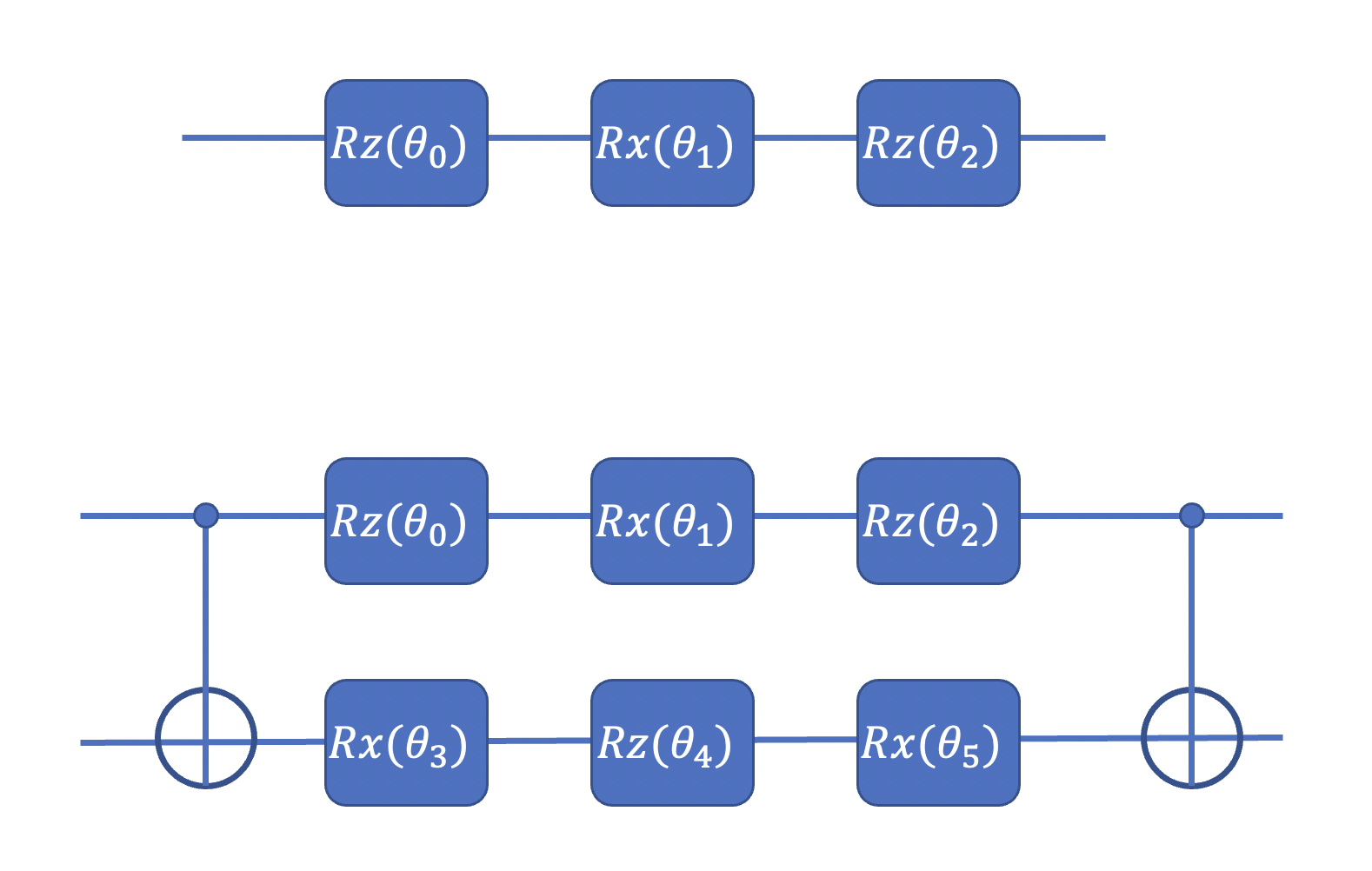
- Randomly choose a block from the 'pool' (As the following figure shows, each block only consists of , , and gates), and insert the block at the end of circuit. Qubits that the block is applied on are also uniformly sampled. The parameters of the inserted gates are initialized to so that the inserted circuit is equivalent to identity.
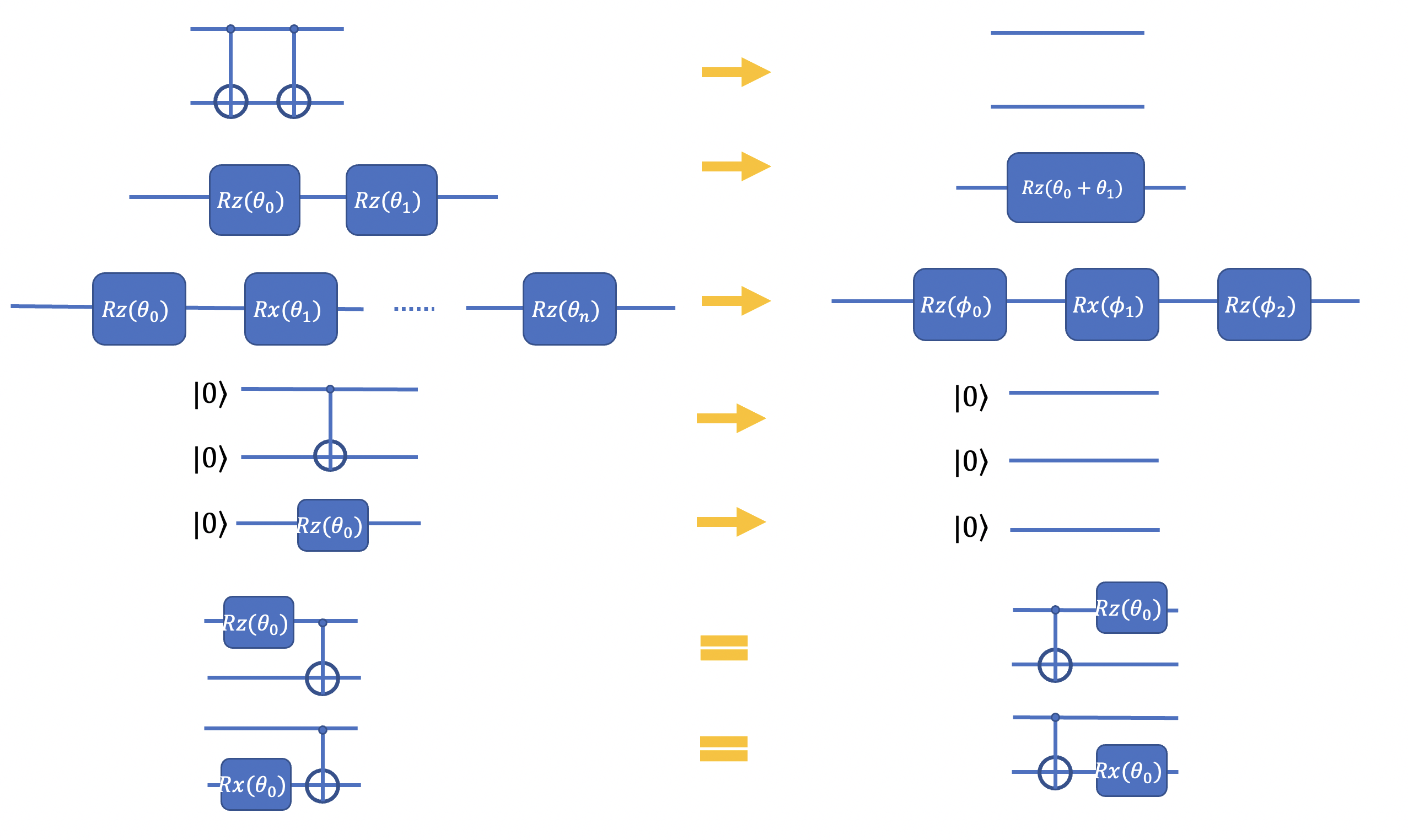
- Simplify the circuit according to the following rules. Run the optimization process, and get the optimal value of loss function. Compare the loss value to the previously stored one, decide whether to accept the new circuit or not according to a pre-defined threshold. If the circuit is accepted, remove gates that do not lower the loss, set the circuit as the current circuit and store the corresponding loss value.
- Repeat steps 2-3 for chosen number of iterations, output the resulting circuit and the optimal loss value.
Paddle Quantum Implementation¶
We consider to get the ground state energy of Hydrogen molecule using Variation Quantum Eigensolver (VQE) together with VAns to optimize the circuit structure as well. First, we import the required packages.
import paddle
import paddle_quantum
import paddle_quantum.qchem as qchem
import numpy as np
from paddle_quantum.ansatz import Circuit
from paddle_quantum.ansatz.vans import Inserter, Simplifier, VAns, cir_decompose
from paddle_quantum.loss import ExpecVal
np.random.seed(11)
paddle.seed(11)
/Users/v_zhanglei48/opt/anaconda3/envs/pq/lib/python3.8/site-packages/paddle/tensor/creation.py:125: DeprecationWarning: `np.object` is a deprecated alias for the builtin `object`. To silence this warning, use `object` by itself. Doing this will not modify any behavior and is safe. Deprecated in NumPy 1.20; for more details and guidance: https://numpy.org/devdocs/release/1.20.0-notes.html#deprecations if data.dtype == np.object: /Users/v_zhanglei48/opt/anaconda3/envs/pq/lib/python3.8/site-packages/paddle/tensor/creation.py:125: DeprecationWarning: `np.object` is a deprecated alias for the builtin `object`. To silence this warning, use `object` by itself. Doing this will not modify any behavior and is safe. Deprecated in NumPy 1.20; for more details and guidance: https://numpy.org/devdocs/release/1.20.0-notes.html#deprecations if data.dtype == np.object:
<paddle.fluid.core_noavx.Generator at 0x7fcf214498f0>
Before using the VAns algorithm, we need to get the Hamiltonian for Hydrogen. Details can be found in the VQE tutorial.
# `driver` is used to calculate various molecular integrals.
driver = qchem.PySCFDriver()
# Build a Molecule class based on its properties, note, the length unit is Angstrom.
mol = qchem.Molecule(
geometry=[("H", [0.0, 0.0, 0.0]), ("H", [0.0, 0.0, 0.74])],
basis="sto-3g",
multiplicity=1,
driver=driver
)
# Recall Hamiltonian
molecular_hamiltonian = mol.get_molecular_hamiltonian()
# n is the number of qubits
n = molecular_hamiltonian.n_qubits
converged SCF energy = -1.11675930739643
Then we define the loss function, which is simply the expectation value of the Hamiltonian.
# Define the loss function
expec_val = ExpecVal(molecular_hamiltonian)
def loss_func(cir: Circuit) -> paddle.Tensor:
return expec_val(cir())
Next, we also need to set some training hyper-parameters before training.
EPSI = 0.001 # set the epsilon
IR = 1 # set the insertion rate
ITERI = 120 # set the number of iterations used for VQE
ITERO = 5 # set the number of iterations used for structure optimization
LR = 0.1 # set the learning rate
T = 0.01 # set the threshold
A = 100 # set the accept wall
IS0 = True # if the initial state is |0>, set to true
paddle_quantum.set_backend('state_vector') # set the backend to state vector
# initialize the framework
vans = VAns(n, loss_func,
epsilon=EPSI,
insert_rate=IR,
iter=ITERI,
iter_out=ITERO,
LR=LR,
threshold=T,
accept_wall=A,
zero_init_state=IS0)
Initial Circuit¶
We give a default initial circuit with uniformly sampled parameters. Then run the optimization process to get the optimal parameters in this initial circuit. The optimization process is the same as in the original VQE. Hyperparameters iter and LR are used in this process.The obtained loss function and the circuit with optimized parameters will be the initial point for the architecture optimization process. Note that the circuit is simplified when we decided to use this optimized circuit as the current starting point. Details of simplification can be found later.
# Optimize the initial circuit
itr_loss = vans.optimization(vans.cir)
# Update the loss
vans.loss = itr_loss
# Print out the current circuit
print("Current circuit is:\n" + str(vans.cir))
/Users/v_zhanglei48/opt/anaconda3/envs/pq/lib/python3.8/site-packages/paddle/fluid/framework.py:1104: DeprecationWarning: `np.bool` is a deprecated alias for the builtin `bool`. To silence this warning, use `bool` by itself. Doing this will not modify any behavior and is safe. If you specifically wanted the numpy scalar type, use `np.bool_` here. Deprecated in NumPy 1.20; for more details and guidance: https://numpy.org/devdocs/release/1.20.0-notes.html#deprecations elif dtype == np.bool:
iter: 20 loss: [-0.99608564]
iter: 40 loss: [-1.0926807]
iter: 60 loss: [-1.1136395]
iter: 80 loss: [-1.116332]
iter: 100 loss: [-1.1167176]
iter: 120 loss: [-1.1167545]
Current circuit is:
--Rx(3.144)----Rz(3.512)----*----Rx(6.286)----Rz(1.375)-------------------------------------------------------------x--
| |
----------------------------x----Rx(4.249)----Rz(3.141)----Rx(4.246)----Rz(5.477)----*------------------------------|--
| |
--Rx(0.001)----Rz(5.499)----*--------------------------------------------------------x----Rx(3.141)----Rz(2.688)----|--
| |
----------------------------x----Rx(0.003)----Rz(2.362)----Rx(0.003)----Rz(1.500)-----------------------------------*--
Insertion¶
Now, we randomly choose a block from the 'pool', and insert the block within the circuit. Qubits that the block is applied on are also uniformly sampled. The parameters of the inserted set of gates are initialized to so that the new circuit can take the advantage of the previously optimized circuit since they act as identity. The code below inserts sets of gates into the circuit. The number of sets of gates depends on the hyperparameter insert_rate. Another hyperparameter epsilon is used to determine the variance from of initial parameters.
# Insert indentity blocks into the current circuit, before doing so, need to
# decompose the circuit from layers to gates
new_cir = cir_decompose(vans.cir)
new_cir = Inserter.insert_identities(new_cir, vans.insert_rate, vans.epsilon)
# Print the updated circuit
print("Circuit after insertion:\n" + str(new_cir))
Circuit after insertion:
--Rx(3.144)----Rz(3.512)----*----Rx(6.286)----Rz(1.375)----------------------------------------------------------------------------------------------------x--
| |
----------------------------x----Rz(0.000)----Rx(0.000)----Rz(-0.00)----Rx(4.249)----Rz(3.141)----Rx(4.246)----Rz(5.477)----*------------------------------|--
| |
--Rx(0.001)----Rz(5.499)----*-----------------------------------------------------------------------------------------------x----Rx(3.141)----Rz(2.688)----|--
| |
----------------------------x----Rx(0.003)----Rz(2.362)----Rx(0.003)----Rz(1.500)--------------------------------------------------------------------------*--
Simplification¶
Then we will simplify the new circuit. Rules are pretty simple:
- Combine consecutive gates.
- Combine rotations gates.
- Remove gates and gates in the front of the circuit if the initial state is .
- Commute rotation gates and gates if the circuit can be further simplified in doing so.
Then we run the parameter optimization process again and get the new minimized value for the loss function. If the new value is smaller than the previous value or the difference between them is smaller than a value that depends on the hyperparameter accept_wall, we accpet the new circuit as the current circuit. After accepting the new circuit, we will remove gates that do not lower the loss or lower the loss within a threshold.
# Simplify the updated circuit according to the simplification rules
new_cir = Simplifier.simplify_circuit(new_cir, vans.zero_init_state)
# Print the simplied circuits
print(new_cir)
# Then optimize the simplified circuits
itr_loss = vans.optimization(new_cir)
# Calculate the change of loss
relative_diff = (itr_loss - vans.loss) / np.abs(itr_loss)
# If the loss is decreased or increased within a threshold, accept the new circuit
if relative_diff <= 0 or np.random.random() <= np.exp(
-relative_diff * vans.accept_wall
):
print("Accpet the new circuit!")
# Remove gates that do not lower the loss
new_cir = vans.delete_gates(new_cir, itr_loss)
new_cir = Simplifier.simplify_circuit(new_cir, vans.zero_init_state)
itr_loss = loss_func(new_cir, *vans.loss_args)
vans.loss = itr_loss
else:
print("Decline the new circuit!")
/Users/v_zhanglei48/opt/anaconda3/envs/pq/lib/python3.8/site-packages/paddle/fluid/dygraph/math_op_patch.py:276: UserWarning: The dtype of left and right variables are not the same, left dtype is paddle.float64, but right dtype is paddle.float32, the right dtype will convert to paddle.float64 warnings.warn(
--Rx(3.144)----Rz(3.512)----*----Rx(6.286)----Rz(1.375)------------------------------------------------x--
| |
----------------------------x----Rz(5.962)----Rx(5.858)----Rz(9.426)----*------------------------------|--
| |
--Rx(0.001)----Rz(5.499)----*-------------------------------------------x----Rx(3.141)----Rz(2.688)----|--
| |
----------------------------x----Rz(3.604)----Rx(5.126)----Rz(4.462)-----------------------------------*--
iter: 20 loss: [-1.104097]
iter: 40 loss: [-1.1159214]
iter: 60 loss: [-1.1165943]
iter: 80 loss: [-1.116723]
iter: 100 loss: [-1.1167536]
iter: 120 loss: [-1.1167593]
Accpet the new circuit!
start deleting gates
Deletion: reject deletion
Deletion: accept deletion with acceptable loss
Deletion: accept deletion with acceptable loss
Deletion: accept deletion with acceptable loss
Deletion: accept deletion with acceptable loss
Deletion: accept deletion with acceptable loss
Deletion: accept deletion with acceptable loss
Deletion: accept deletion with acceptable loss
Deletion: accept deletion with acceptable loss
Deletion: accept deletion with acceptable loss
Deletion: accept deletion with acceptable loss
Deletion: reject deletion
Deletion: accept deletion with acceptable loss
Deletion: accept deletion with acceptable loss
12 gates are deleted!
Then we update the current circuit to the new circuit.
# Update the current circuit
vans.cir = new_cir
print("The current circuit:\n" + str(vans.cir))
The current circuit:
--Rx(3.141)----*----------------------x--
| |
---------------x----*-----------------|--
| |
--------------------x----Rx(3.142)----|--
|
--------------------------------------*--
The insertion and simplification together forms one iteration for the architecture optimization process. The number of iterations is determined by the hyperparameter iter_out.
Simple version¶
While you can customize your own optimization process by adjusting insertion and simplification processes and implementing the training process, Paddle Quantum provides an elegant version of VAns. You can complete the architecture optimization all at once.
# optimization process all at once
vans.train()
Out iteration 1 for structure optimization:
iter: 20 loss: [-1.1167216]
iter: 40 loss: [-1.1166946]
iter: 60 loss: [-1.1167494]
iter: 80 loss: [-1.1167588]
iter: 100 loss: [-1.1167591]
iter: 120 loss: [-1.1167594]
Current loss: [-1.1167594]
Current cir:
--Rx(3.141)----*----------------------x--
| |
---------------x----*-----------------|--
| |
--------------------x----Rx(3.141)----|--
|
--------------------------------------*--
Out iteration 2 for structure optimization:
iter: 20 loss: [-1.1363345]
iter: 40 loss: [-1.1367742]
iter: 60 loss: [-1.137219]
iter: 80 loss: [-1.1372814]
iter: 100 loss: [-1.1372831]
iter: 120 loss: [-1.1372838]
accpet the new circuit!
start deleting gates
Deletion: reject deletion
Deletion: accept deletion with acceptable loss
Deletion: reject deletion
Deletion: accept deletion with acceptable loss
Deletion: accept deletion with acceptable loss
Deletion: accept deletion with acceptable loss
Deletion: accept deletion with acceptable loss
Deletion: reject deletion
Deletion: accept deletion with acceptable loss
Deletion: accept deletion with acceptable loss
Deletion: accept deletion with acceptable loss
Deletion: accept deletion with acceptable loss
Deletion: reject deletion
Deletion: accept deletion with acceptable loss
10 gates are deleted!
Current loss: -1.126142144203186
Current cir:
--Rx(3.141)----*------------------------------------*---------------------*----x--
| | | |
---------------x----*----Rx(0.226)----*----*--------x--------Rz(-0.81)----x----|--
| | | |
--------------------|-----------------|----x----Rx(3.141)----------------------|--
| | |
--------------------x-----------------x----------------------------------------*--
Out iteration 3 for structure optimization:
iter: 20 loss: [-1.1365268]
iter: 40 loss: [-1.1370414]
iter: 60 loss: [-1.1372557]
iter: 80 loss: [-1.1372817]
iter: 100 loss: [-1.1372832]
iter: 120 loss: [-1.1372838]
accpet the new circuit!
start deleting gates
Deletion: reject deletion
Deletion: reject deletion
Deletion: accept deletion with acceptable loss
Deletion: accept deletion with acceptable loss
Deletion: accept deletion with acceptable loss
Deletion: accept deletion with acceptable loss
Deletion: accept deletion with acceptable loss
Deletion: accept deletion with acceptable loss
Deletion: reject deletion
Deletion: reject deletion
6 gates are deleted!
Current loss: -1.1340010166168213
Current cir:
--Rx(3.141)----*------------------------------------*---------------------*----x--
| | | |
---------------x----*----Rx(0.225)----*----*--------x--------Rz(-1.16)----x----|--
| | | |
--------------------|-----------------|----x----Rx(3.141)----------------------|--
| | |
--------------------x-----------------x----------------------------------------*--
Out iteration 4 for structure optimization:
iter: 20 loss: [-1.1371578]
iter: 40 loss: [-1.1371865]
iter: 60 loss: [-1.1372653]
iter: 80 loss: [-1.1372821]
iter: 100 loss: [-1.1372833]
iter: 120 loss: [-1.137284]
accpet the new circuit!
start deleting gates
Deletion: reject deletion
Deletion: reject deletion
Deletion: reject deletion
Deletion: reject deletion
Deletion: accept deletion with acceptable loss
Deletion: accept deletion with acceptable loss
Deletion: accept deletion with acceptable loss
3 gates are deleted!
Current loss: -1.135810136795044
Current cir:
--Rx(3.141)----*------------------------------------*---------------------*----x--
| | | |
---------------x----*----Rx(0.225)----*----*--------x--------Rz(-1.30)----x----|--
| | | |
--------------------|-----------------|----x----Rx(3.141)----------------------|--
| | |
--------------------x-----------------x----------------------------------------*--
Out iteration 5 for structure optimization:
iter: 20 loss: [-1.1363769]
iter: 40 loss: [-1.1369352]
iter: 60 loss: [-1.1372398]
iter: 80 loss: [-1.137279]
iter: 100 loss: [-1.1372832]
iter: 120 loss: [-1.1372834]
accpet the new circuit!
start deleting gates
Deletion: reject deletion
Deletion: accept deletion with acceptable loss
Deletion: accept deletion with acceptable loss
Deletion: accept deletion with acceptable loss
Deletion: accept deletion with acceptable loss
Deletion: accept deletion with acceptable loss
Deletion: reject deletion
Deletion: reject deletion
Deletion: reject deletion
Deletion: accept deletion with acceptable loss
Deletion: accept deletion with acceptable loss
Deletion: accept deletion with acceptable loss
8 gates are deleted!
Current loss: -1.135881781578064
Current cir:
--Rx(3.141)----*------------------------------------*---------------------*----x--
| | | |
---------------x----*----Rx(0.226)----*----*--------x--------Rz(-1.30)----x----|--
| | | |
--------------------|-----------------|----x----Rx(3.141)----------------------|--
| | |
--------------------x-----------------x----------------------------------------*--
The final loss: -1.135881781578064
The final circuit:
--Rx(3.141)----*------------------------------------*---------------------*----x--
| | | |
---------------x----*----Rx(0.226)----*----*--------x--------Rz(-1.30)----x----|--
| | | |
--------------------|-----------------|----x----Rx(3.141)----------------------|--
| | |
--------------------x-----------------x----------------------------------------*--
The final circuit we got from VAns is
print("Final circuit:\n" + str(vans.cir))
print("Final loss:\n" + str(vans.loss))
Final circuit:
--Rx(3.141)----*------------------------------------*---------------------*----x--
| | | |
---------------x----*----Rx(0.226)----*----*--------x--------Rz(-1.30)----x----|--
| | | |
--------------------|-----------------|----x----Rx(3.141)----------------------|--
| | |
--------------------x-----------------x----------------------------------------*--
Final loss:
-1.135881781578064
Comparison with original VQE¶
The circuit we got using VAns consists of only 5 parameters and the depth of the circuit is 9. The minimized loss value is Ha. Comparing to the fixed ansatz used in the original VQE tutorial, where the circuit consists of 12 parameters and with depth 11, VAns reduces the number of parameters needed while keeps the circuit shallower.
References¶
[1] Bilkis, M., et al. "A semi-agnostic ansatz with variable structure for quantum machine learning." arXiv preprint arXiv:2103.06712 (2021).