Quantum Phase Processing

Copyright (c) 2022 Institute for Quantum Computing, Baidu Inc. All Rights Reserved.

Overview

Quantum Phase Processing (QPP) is a quantum algorithmic structure purposed by the Baidu Research team [1]. Such structure can provide access to the eigenphases of the target unitary, allowing phase transformation or extraction to be done in an efficient and precise manner. QPP originates from an improved technique known as Trigonometric Quantum Signal Processing (namely the trigonometric QSP) [2] that can simulate arbitrary trigonometric transformation of input data using only one qubit. Consequently, QPP inherits the capability of trigonometric QSP in a higher dimension. By manipulating the input unitary, QPP can retrieve its eigen-information and hence perform trigonometric transformation to each eigenphase insider the corresponding eigenspace.

This tutorial will illustrate how to utilize QPP to resolve the problems of quantum phase estimation, Hamiltonian simulation and entropy estimation, according to the paper [1] and the idea of block encoding.

Here are some necessary libraries and packages.

import warnings
warnings.filterwarnings("ignore")

import numpy as np
from scipy.linalg import expm
import paddle

# general functions in PaddleQuantum
import paddle_quantum as pq
from paddle_quantum.hamiltonian import Hamiltonian
from paddle_quantum.linalg import abs_norm, hermitian_random, unitary_random, block_enc_herm, herm_transform, is_density_matrix
from paddle_quantum.qinfo import trace_distance, partial_trace_discontiguous
from paddle_quantum.state import random_state, zero_state, State

# functions in QPP module
from paddle_quantum.qpp import Q_generation, hamiltonian_laurent, qpp_angle_approximator, qpp_cir, qps, purification_block_enc, simulation_cir

# set the precision
pq.set_dtype('complex128')

/Users/v_zhanglei48/opt/anaconda3/envs/pq/lib/python3.8/site-packages/paddle/tensor/creation.py:125: DeprecationWarning: `np.object` is a deprecated alias for the builtin `object`. To silence this warning, use `object` by itself. Doing this will not modify any behavior and is safe. 
Deprecated in NumPy 1.20; for more details and guidance: https://numpy.org/devdocs/release/1.20.0-notes.html#deprecations
  if data.dtype == np.object:

Introduction of QPP Structure

QPP relies on a quantum circuit namely the quantum phase processor to deal with quantum data. For even $L \in \mathbb{N}$, we define the quantum phase processor of an $n$-qubit unitary $U$ as

$$ V^L(U) := R_z^{(0)} R_y^{(0)} R_z^{(0)} \left[ \prod_{l=1}^{L/2} \begin{bmatrix} U^\dagger & 0 \\ 0 & I^{\otimes n} \end{bmatrix} R_y^{(0)} R_z^{(0)} \begin{bmatrix} I^{\otimes n} & 0 \\ 0 & U \end{bmatrix} R_y^{(0)} R_z^{(0)} \right], \tag{1} $$

Here $R_y^{(0)}$ and $R_z^{(0)}$ are rotation gates applied on the first qubit with tunable parameters depending on the target trigonometric polynomial. The quantum circuit of $V^L(U)$ is shown as follows:

Note：when the number of layers $L$ is odd, we define the corresponding phase processor as

$$ V^{L}(U) = V^{L - 1}(U) \begin{bmatrix} U^\dagger & 0 \\ 0 & I^{\otimes n} \end{bmatrix} R_y^{(0)} R_z^{(0)}. \tag{2} $$

QPP has two main functionals: phase evolution and phase estimation. Suppose we have an $n$-qubit unitary with the following spectrum decomposition

$$ U = \sum_{j=0}^{2^n - 1} e^{i \tau_j} |\chi_j \rangle \langle \chi_j |. \tag{3} $$

Then by Theorem 5 in [1], for any (complex) trigonometric polynomial $F(x) = \sum_{j = -L}^L c_j e^{ijx}$ such that $||\textbf{c}||_1 \leq 1$, and any quantum state $| \psi \rangle = \sum_{j=0}^{2^n - 1} \alpha_j |\chi_j \rangle$, there exists a quantum phase processor $V^{2L}(U)$ of $2L$ layers such that

$$ \left( \langle 0 | \otimes I^{\otimes n} \right) V^{2L}(U) |0, \psi \rangle = \sum_{j=0}^{2^n - 1} \alpha_j F(\tau_j) | \chi_j \rangle. \tag{4} $$

Further, suppose $F$ is real-valued. Then for any state $\rho$, by Theorem 6 in [1] there exists a quantum phase processor $V^{L}(U)$ of $L$ layers

$$ \text{Tr} \left[ Z^{(0)} \cdot V^{L}(U) \rho V^{L}(U)^\dagger \right] = \sum_{j = 0}^{2^n - 1} p_j F(\tau_j), \tag{5} $$

where $p_j = \langle \chi_j | \rho | \chi_j \rangle$ and $Z^{(0)}$ is the Pauli-$Z$ observable acting on the first qubit. In this tutorial we wil use these two abilities to complete the eigenphase search of unitary, the real-time evolution of Hamiltonian and the trace estimation of function transformation of quantum states.

Note: Since Hamiltonian and quantum states are not unitaries, and hence cannot be processed by QPP directly. Therefore, we need to use the qubitized block encoding to get the eigen-information of non-unitary data. Besides, there is an $\arccos$ relation between eigenphases of qubitized block encoding and eigenvalues of its encoded data. Then to perform a transformation of function $f$, QPP needs to simulate $F(x) = f(\cos(x))$.

See more details of block encoding in the tutorial of Quantum Signal Processing and Quantum Singular Value Transformation. The idea of qubitized block encoding is deferred to [1] and [3].

Here is the environment setup of this tutorial.

num_qubits = 3 # size of main register
num_block_qubits = num_qubits + 1 # number of ancilla qubits used in block encoding
aux_qubits = list(range(num_block_qubits + 1)) # qubit indexes for auxiliary register
sys_qubits = list(range(num_block_qubits + 1, num_block_qubits + 1 + num_qubits)) # qubit indexes for main register

Application: Quantum Phase Search

Finding eigenphases of a unitary is one of the fundamental issues in quantum computation, namely the problem of quantum phase estimation. The setup of this problem is as follows: given a unitary $U$ and its eigenstate $| \psi \rangle$, estimate the eigenphase corresponding to $| \psi \rangle$; further, if $| \psi \rangle$ is no longer an eigenstate of $U$, then estimate the eigenphase corresponding to a eigenstate having non-zero overlap with $| \psi \rangle$.

Here is the experimental setup of this problem.

pq.set_backend('state_vector') # switch to state vector backend

U = unitary_random(num_qubits) # input unitary
psi = random_state(num_qubits) # input state (vector)

QPP can simulate ladder function i.e.

$$ f(x) = \begin{cases} 1 & \textrm{if }\, x \geq 0 \\ 0 & \textrm{if }\, x < 0 \end{cases}. \tag{6} $$

Through indirect measurements, binary searches are applied to locate a small interval containing an eigenphase of $U$; this interval is then expanded such that binary search can be used again. Such method is called the quantum phase search (QPS) algorithm. Compared with conventional QPE algorithm, QPS can achieve exponential enhancement on the success probability, under same precision and resource usage. Details of QPS is deferred to section 2 of paper [1].

The QPP module of Paddle Quantum has a built-in function qps that can realize the QPS algorithm. We can compare the experimental result with theoretical one to verify the correction of this method.

# Use QPS algorithm to retrieve an eigenphase and its output state
phase_estimate, output_state = qps(U, psi)

# Compute the eigenphase corresponding to the output state
phase_expect = np.log((output_state.bra @ U @ output_state.ket).item()) / 1j

print(f"The searching error for the QPS algorithm is {np.abs(phase_expect - phase_estimate)}")
print(f"The overlap between input and output states is {abs_norm(output_state.bra @ psi.ket)}")

Computations of angles for QPP are completed with mean error 2.8162115647895675e-07
The searching error for the QPS algorithm is 4.606981463737032e-12
The overlap between input and output states is 0.37013326587541756

As shown above, despite that $| \psi \rangle$ is not an eigenstate of $U$, we can still find an eigenphase and its corresponding eigenstate having non-zero overlap with $| \psi \rangle$.

Application: Hamiltonian Simulation

The time evolution of an $n$-qubit quantum system is decided by a Hamiltonian $H$ (a $2^n \times 2^n$ Hermitian matrix acting on $n$ qubits) and an initial state $\rho$. The quantum state of this system at time $t$ can be expressed as $\rho_t = e^{-iHt} \rho e^{iHt}$, where $e^{-iHt}$ is the evolution operator at time $t$. Then the problem of Hamiltonian simulation can be formulated as follows: given a block encoding of the Hamiltonian of a quantum system and its initial state $\rho$, prepare the quantum state $\rho_t$ of this system at time $t$.

Here is the experimental setup of this problem.

pq.set_backend("density_matrix") # switch to density matrix backend

H = hermitian_random(num_qubits) # Hamiltonian of quantum system
U = block_enc_herm(H, num_block_qubits) # qubitized block encoding of the Hamiltonian
rho = random_state(num_qubits) # initial state
t = 9 # evolution time
L = 40 # number of layers of quantum phase processor i.e. degree of simulation precision

In QPP module, from the Jacobi-Anger expansion, function hamiltonian_laurent can provide a trigonometric polynomial $P$ approximating the evolution function. Then we can use Q_generation to calculate its polynomial complement $Q$ (that satisfies $PP^* + QQ^* = 1$). After estimating the angles for rotation gates by qpp_angle_approximator, qpp_cir will eventually give a quantum realization of the quantum phase processor.

# Prepare the trigonometric poly approximating the evolution function, and its complement;
#   here we multiply P by constant slightly smaller than 1 to ensure the computation of Q
P = hamiltonian_laurent(-t, L) * 0.999999
Q = Q_generation(P)

# Compute the rotation angles, where theta/phi corresponds to Ry/Rz gates
list_theta, list_phi = qpp_angle_approximator(P, Q)

cir = qpp_cir(list_theta, list_phi, U) # construct quantum phase processor构建相位处理器
cir.collapse(aux_qubits, desired_result=0, if_print=True) # decoding (measurement) of the block encoding 
input_state = zero_state(num_block_qubits + 1).kron(rho) # prepare the input state, where input state for aux reg is |0><0|

Computations of angles for QPP are completed with mean error 2.477981491445382e-07

# Get the output state, remove the aux qubits, and compare the output state with the expected one
output_state = partial_trace_discontiguous(cir(input_state), preserve_qubits=sys_qubits)
rho.evolve(H, t)
print(f"The trace distance between output and expected states is {trace_distance(output_state, rho).item()}")

qubits [0, 1, 2, 3, 4] collapse to the state |00000> with probability 0.9999974886442893
The trace distance between output and expected states is 4.4205432295805146e-07

As shown above, through phase evolution, QPP transform a block encoding of $H$ to a block encoding of $e^{-iHt}$, so that $\rho_t$ is successfully prepared.

Application: Estimation of Quantum Entropies

Trace computation of function transformation of quantum states is the core component of quantum entropy estimation. The mathematical setting of this problem is as follows: given two quantum states $\rho, \sigma$ and a function $f:~\mathbb{R}_+~\to~\mathbb{R}$, estimate the quantity $\text{Tr}\left[ \rho f \left( \sigma \right) \right]$.

Note：$f$ transformation of quantum state $\sigma$ is defined as

$$ f(\sigma) = \sum_j f(q_j) | \psi_j \rangle \langle \psi_j |, \tag{7} $$

where $\{q_j\}$ and $\{ | \psi_j \rangle \}$ are eigenvalues and eigenstates of $\sigma$, respectively.

We can observe that, if $f$ is a power function, then the solution of this problem can estimate quantum Rényi entropies and Rényi divergences; if $f(x) = \log(x)$, such problem is equivalent to the estimation of quantum Von Neumann or relative entropies.

QPP can efficiently solve the trace estimation problem by phase estimation, so that serval quantum entropies can be estimated. The quantum circuit is shown as follows:

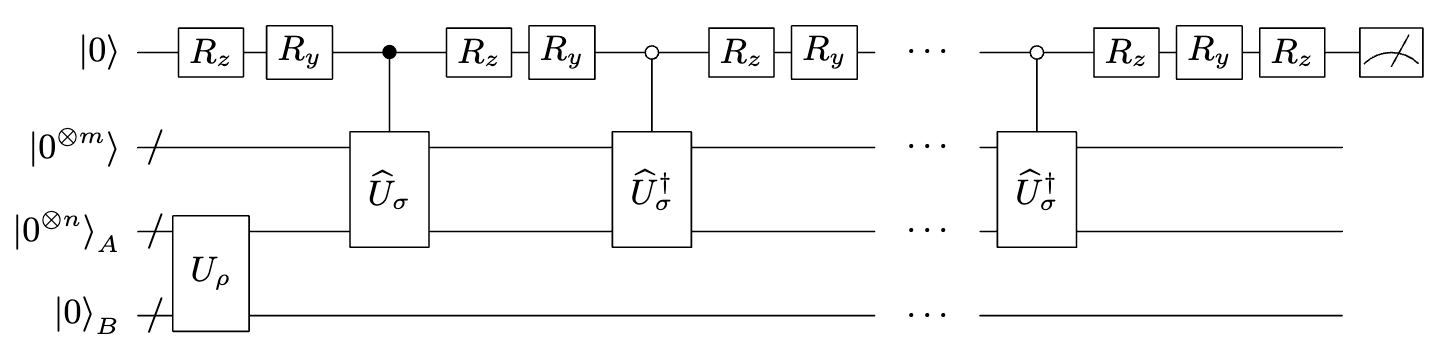
Here $U_\rho$ acting on AB systems is the purification model of $\rho$, satisfying

$$ \text{Tr}_B \left[ U_\rho \left( | 0 \rangle_A \langle 0 |_A \otimes | 0 \rangle_B \langle 0 |_B \right) U_\rho^\dagger \right] = \rho. \tag{8} $$

Such model can be realized by quantum realized, and are frequently used in the study of quantum entropies. $U_\sigma$ is also the purification model of $\sigma$. However, to obtain the eigen-information of $\sigma$, QPP further transforms $U_\sigma$ to the block encoding $\widehat{U}_\sigma$ of $\sigma$. See more details in section 4 of paper [1].

We will use above circuit to estimate $\text{Tr} \left[ \rho \sigma^{\alpha - 1} \right]$. Here is the experimental setup of this problem.

pq.set_backend("density_matrix") # switch to density matrix backend

rho = random_state(num_qubits) # quantum state rho, here we don't care about the system B
U_sigma_hat = purification_block_enc(num_qubits, num_block_qubits) # construct a qubitized block encoding of (random) purification model
sigma = State(U_sigma_hat[:2**num_qubits, :2**num_qubits]) # obtain sigma by block encoding
assert is_density_matrix(sigma) == (True, num_qubits)

alpha = np.random.rand() * 4 + 1 # randomly select alpha in [1, 5)
H = Hamiltonian([(1.0, "z0")]) # Pauli-Z observable acting on the first qubit
input_state = zero_state(num_block_qubits + 1).kron(rho) # input state for the phase processor

The built-in function simulation_cir in QPP module can design adaptive phase processor for function $f$. In particular, by finding the trigonometric polynomial $F$ approximating the function $f$. QPP module can transform $F$ to the trigonometric polynomial that phase processor needs to simulate, under machinery error. Then the final result can be obtained by computing the expectation value of Pauli-Z observable acting on the first qubit. We can utilize paddle_quantum.linalg.herm_transform to assess the simulation precision.

Note: function $f$ needs to satisfy $f\left(\left[0, 1\right]\right) \subseteq \left[-1, 1\right]$.

# Estimate Tr[rho * sigma^(alpha - 1)]
cir = simulation_cir(lambda x: (np.cos(x) ** 2) ** ((alpha - 1) / 2), U_sigma_hat)
val = cir(input_state).expec_val(H)
expect_val = paddle.trace(rho.data @ herm_transform(lambda x: x ** (alpha - 1), sigma)).real().item()
print(f"The estimation error for Tr[rho * sigma^{alpha - 1}] is {np.abs(val - expect_val)}")

Computations of angles for QPP are completed with mean error 3.3321641726764387e-07
The estimation error for Tr[rho * sigma^2.0113183131522914] is 3.2651025185431726e-05

As shown above, through phase estimation, QPP can precisely estimate $\text{Tr} \left[ \rho \sigma^{\alpha - 1} \right]$. Therefore, when $\rho = \sigma$, QPP is capable to estimate the $\alpha$-Rényi entropy of $\rho$, defined as

$$ S_\alpha(\rho) = \frac{1}{1 - \alpha}\log \text{Tr} \left( \rho^{\alpha } \right). \tag{9} $$

Conclusion

Through above applications, this tutorial demonstrates that QPP structure is capable of solving problems of unitaries, Hamiltonians and quantum states. Other than applications mentioned in this tutorial, we expect to use such framework to QPP can be potentially applied to other problems, including but not limited to problems of quantum Monte Carlo, unitary trace estimation and machine learning.

---

Reference

[1] Wang, Xin, et al. "Quantum Phase Processing: Transform and Extract Eigen-Information of Quantum Systems." arXiv preprint arXiv:2209.14278 (2022).

[2] Yu, Zhan, et al. "Power and limitations of single-qubit native quantum neural networks." arXiv preprint arXiv:2205.07848 (2022).

[3] Low, Guang Hao, and Isaac L. Chuang. "Hamiltonian simulation by qubitization." Quantum 3 (2019): 163.