Quantum Signal Processing and Quantum Singular Value Transformation¶

Copyright (c) 2022 Institute for Quantum Computing, Baidu Inc. All Rights Reserved.

Overview¶

Quantum signal processing (QSP), originally purposed by Guang Hao Low and Issac L. Chuang [1], is an algorithm for simulation of polynomial transformation of scalars using reflection ($R_X$) and rotation ($R_Z$) operators. QSP states that, for a specific group of polynomials like the Chebyshev polynomials of the first kind, such simulation can be done by a single qubit. Moreover, using a technique called "linear combination of unitaries", we can use two more ancilla qubit to simulate all complex polynomials and hence approximate any functions that can be expanded by Taylor series.

The idea of QSP is further generalized by paper [2], so that it can simulate polynomial transformation of matrices using high-dimensional rotation operators. Since the polynomial transformation of a diagonalizable matrix is intrinsically the polynomial transformation of its singular values, this algorithm is called the quantum singular value transformation (QSVT).

Moreover, a technique called qubitization is further employed to substantially reduce the complexity of high-dimensional rotation operators, so that one (ancilla) qubit suffices to perform the rotation in larger space.

Based on paper [2], this tutorial will illustrate quantum signal processing, quantum singular value transformation and qubitization, and how to implement these algorithms in PaddleQuantum. But first of all, we need to present the idea of block encoding.

Here are some necessary libraries and packages.

Block Encoding¶

Block encoding is a method to encode matrices of data. In quantum computing, for a matrix $A\in C^{2^n\times 2^n}$, a unitary $U\in C^{2^m\times 2^m}$ is said to be a block encoding of $A$ if there exists two orthogonal projectors $W,V\in C^{2^m\times 2^m}$ such that

This could appear more familiar when $W=V=|0{⟩}^{\otimes (m-n)}⟨0{|}^{\otimes (m-n)}\otimes I^{\otimes n}$, where above equation implies

That is, $A$ is the left-upper block of matrix $U$.

Encoding and Decoding of Matrices¶

There are numerous ways to find a block encoding unitary $U$ of a matrix $A$. For example, when $A$ is diagonalizable, $U$ can be constructed as

when $A$ is a unitary, we can simply select $U=A\oplus I^{\otimes (m-n)}$ i.e. $U$ is a controlled $A$. Despite the fact that we do not hold a mature method for doing this in a quantum system, several studies [3] [4] have been conducted on the quantum implementation of block encodings. In this tutorial, we will assume that there exists an efficient algorithm to block encode a matrix (or at least a Hermitian matrix) in a quantum circuit.

Realization in PaddleQuantum.¶

As for the decoding part, the information of matrix $A\in C^{2^n\times 2^n}$ can be extracted by applying its block encoding unitary $U\in C^{2^m\times 2^m}$ on $|0{⟩}^{\otimes (m-n)}⟨0{|}^{\otimes (m-n)}\otimes \rho$, where $\rho$ is an $n$-qubit quantum state. Then the output state is

Measuring the first quantum register with outcome $0^{\otimes (m-n)}$ gives the desired information.

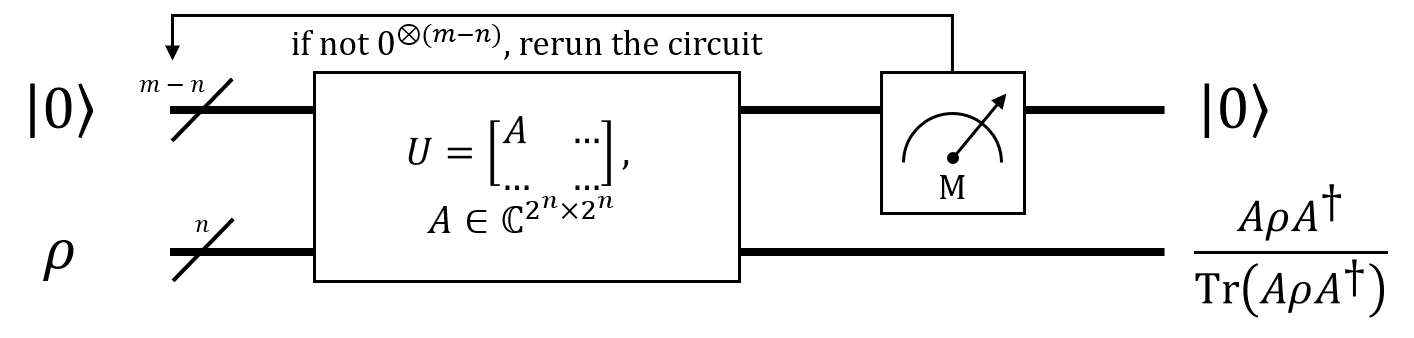
The success probability of decoding is the probability of measuring $0^{\otimes (m-n)}$, which can be exponentially small as $m-n$ increases. However, this would no longer be a problem if we can control the size of first register. In this tutorial we will assume $m=n+1$.

We can verify that the output_rho is the same as $\frac{A\rho A^{†}}{\text{Tr}\left(A\rho A^{†}\right)}$.

When $m=1$ (and hence $n=0$), $A$ is a scalar. In this case we can calculate the expectance of $U$ in terms of state $|0⟩$ to receive $A$.

Quantum Signal Processing¶

Theorem 3-4 in paper [2] state that, for a polynomial $P\in C\left[x\right]$ with $\mathrm{deg}\left(P\right)=k$ that satisfies

• if $k$ is even/odd, then $P$ is a even/odd polynomial;
• $|P\left(x\right)|\le 1,\forall x\in [-1,1]$;
• $|P\left(x\right)|\ge 1,\forall x\in (-\infty ,-1]\cup [1,\infty )$;
• if $k$ is even, then $P\left(ix\right)P^{\ast }\left(ix\right)\ge 1$,

there exists a polynomial $Q\in C\left[x\right]$ and a vector of angles $\Phi =({\varphi }_0,...,{\varphi }_k)\in R^{k+1}$ such that $\forall x\in [-1,1]$,

That is, we can use $k+1$ rotation ($R_Z$) gates and $k$ reflection ($R_X$) gates to receive a block encoding unitary $W_{\Phi }\left(x\right)$ of $P\left(x\right)$. After block decoding we have completed the simulation of $P\left(x\right)$.

Here are some polynomials that satisfy above requirements.

Note that such structure of $W_{\Phi }$ naturally fits the family of Chebyshev polynomials. Indeed, for a Chebyshev polynomials of first kind with order $k$, its corresponding $\Phi$ is $(0,\pi ,...,\pi )$ (if $k$ is even) or $(\pi ,...,\pi )$ (if $k$ is odd).

PaddleQuantum has a built-in class ScalarQSP for quantum signal processing and a function Phi_verification to verify whether $W_{\Phi }$ is a block encoding of $P$.

We can also verify the correctness of $\Phi$ from the corresponding circuit.

Variant of QSP¶

Moreover, the number of parameters can be further simplified to $k$ by finding a vector of angles $\Phi \in R^k$ such that

where

In PaddleQuantum, we can compute such $\Phi$ by function reflection_based_quantum_signal_processing.

Note: $R_{-\Phi }\left(x\right)$ is a block encoding of $P^{\ast }\left(x\right)$.

Quantum Singular Value Transformation¶

To start with, we need to define the singular value transformation.

Let $X\in C^{2^m\times 2^m}$ be a matrix. Suppose there exists a unitary $U$ and two orthogonal projectors $W$ and $V$ such that $X=WUV$. Then there exists two orthonormal basis $\{|{\omega }_j⟩{\}}_{j=1}^{2^m}$ and $\{|{\nu }_j⟩{\}}_{j=1}^{2^m}$ extended by eigenstates of $W$ and $V$ respectively, such that

where

is a singular value of $X$. The singular value transformation (SVT) of $X$ for a function $f$ is defined to be

Decomposition and QSP¶

Paper [2] proves that under appropriate choices of basis, $U,V$ and $W$ can be decomposed by subspaces of ${\lambda }_j$ such that

We can decompose $f^{\left(SV\right)}$ in a similar manner.

Let's connect above decomposition with quantum signal processing. Suppose function $f$ is a polynomial $P\in C\left[x\right]$ with degree $k$ that satisfies the requirements in the last section. Then there exists $\Phi \in R^k$ such that $R_{\Phi }$ is a block encoding of $P$. Moreover, $P$ satisfies $P\left(1\right)=e^{i{\sum }_{j=1}^k{\varphi }_j}$ and $P\left(0\right)=e^{i{\sum }_{j=1}^k(-1{)}^{j+1}{\varphi }_j}$. Now Define $U_{\Phi }$ as

Then

and hence

If we can realize $V{U}_{\Phi }V$ or $W{U}_{\Phi }V$ by a quantum algorithm, then such transformation is the quantum singular value transformation of $X$.

QSVT and Block Encoding¶

Suppose $U$ is a block encoding unitary of $A$ with respect to orthogonal projectors $W$ and $V$. Then $X=A\oplus 0I^{\otimes (m-n)}$ and $P^{\left(SV\right)}\left(X\right)=P^{\left(SV\right)}\left(A\right)\oplus 0I^{\otimes (m-n)}$. Therefore, $U_{\Phi }$ is a block encoding of $P^{\left(SV\right)}\left(A\right)$.

When $W=V$, $\{|{\omega }_j⟩{\}}_{j=1}^{2^m}=\{|{\nu }_j⟩{\}}_{j=1}^{2^m}$. Denote $P\left(x\right):={\sum }_{i=0}^k{c}_i{x}^i$. We can find that

That is, when $W=V$, QSVT maps a block encoding of $A$ to a block encoding of $P\left(A\right)$.

PaddleQuantum has a built-in class QSVT for quantum singular value transformation when $W=V=|0{⟩}^{\otimes (m-n)}⟨0{|}^{\otimes (m-n)}\otimes I^{\otimes n}$. We can call its member function QSVT.block_encoding_matrix() to verify the correctness of above theories, from entries to entries and from eigenvalues to eigenvalues.

Qubitization: Quantum Realization of $U_{\Phi }$¶

One question is, how to realize $U_{\Phi }$ by a quantum circuit? Note that we assume $U$ is implementable. Then the remaining problem is the realization of unitaries $e^{i\varphi (2W-I)}$ and $e^{i\varphi (2V-I)}$, which are essentially $R_Z(-2\varphi )$ operators performed in projection spaces of $W$ and $V$ respectively.

To achieve this, Lemma 10 in paper [1] projects the image space of projector into an ancilla qubit and perform the rotation operation on that qubit. Then by entanglement such rotation is simultaneously applied to the main register.

The results are summarized to the following circuit:

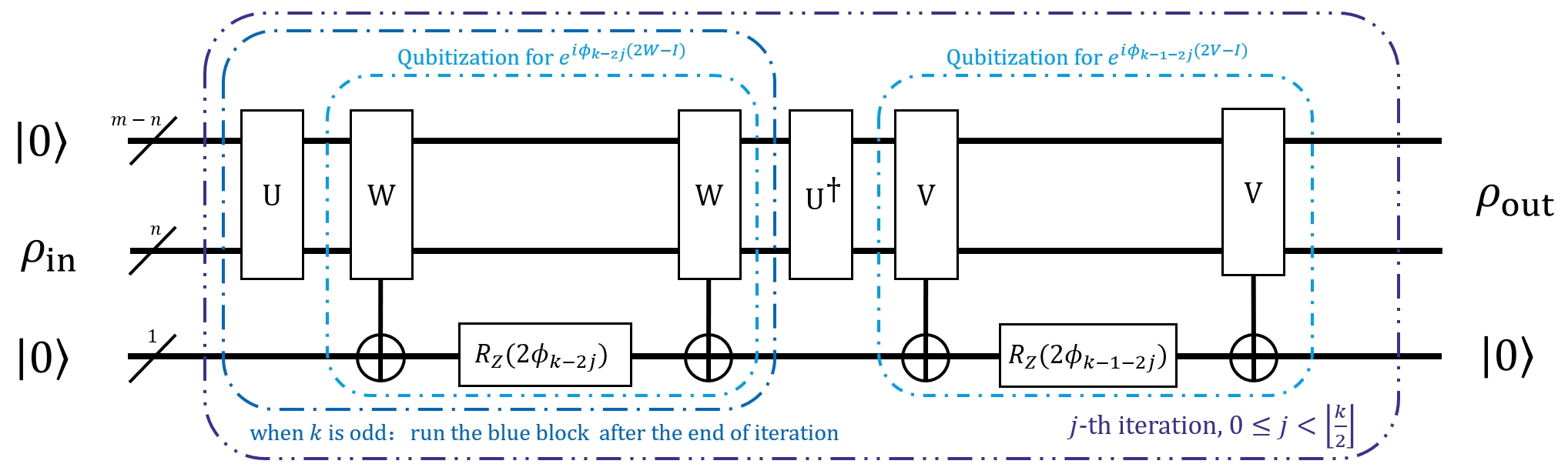
When $W=V=|0{⟩}^{\otimes (m-n)}⟨0{|}^{\otimes (m-n)}\otimes I^{\otimes n}$, PaddleQuantum can create a circuit in Figure 2 by member function QSVT.block_encoding_circuit. We can show that the constructed quantum circuit can simulate $U_{\Phi }$, by comparison of the output state and $(U_{\Phi }\otimes I)|\psi ⟩|0⟩$ for $|\psi ⟩\in C^{2^m}$.

Note: if we add Hadamard gates at the beginning and the end of the ancilla register in Figure 2, then the quantum circuit turns to simulate the real part of the polynomial. Combined with the technique of linear combination of unitaries, theocratically we can simulate all complex polynomials with norm smaller than 1 using quantum circuit.

Application: Amplitude Amplification¶

Let $|\psi ⟩$ be a $m$-qubit quantum state such that $|\psi ⟩=\sin \left(\theta \right)|{\psi }_{\text{good}}⟩+\cos \left(\theta \right)|{\psi }_{\text{bad}}⟩$. Amplitude amplification is a quantum algorithm that can increase the amplitude of $|{\psi }_{\text{good}}⟩$ to approximately 1. This algorithm can be viewed in a different prospective. Let $U$ be the unitary and $W,V$ be two orthogonal projectors such that $|\psi ⟩=UV|0{⟩}^{\otimes m}$ and $\sin \left(\theta \right)|{\psi }_{\text{good}}⟩=W|\psi ⟩$, implying $\sin \left(\theta \right)|{\psi }_{\text{good}}⟩=WUV|0{⟩}^{\otimes m}$. Therefore, amplitude amplification is essentially a singular value transformation of $X=WUV$. In this section we will show how to use QSVT to do fixed-point (i.e. $\theta =\frac{\pi }{2k}$ for some $k\in Z$) amplitude amplification from Theorem 28 of paper [2].

Suppose $\sin \left(\theta \right)|{\psi }_{\text{bad}}⟩=(|{\psi }_{\text{good}}{⟩}^{\otimes (m-n)}⟨0{|}^{\otimes (m-n)}\otimes I^{\otimes n})|\psi ⟩$ and $\theta =\frac{\pi }{2k}$ for some $k\in Z$. Then $W=V=|0{⟩}^{\otimes (m-n)}⟨0{|}^{\otimes (m-n)}\otimes I^{\otimes n}$ and $X=A\oplus 0I^{\otimes (m-n)}$, where $A$ is the left-upper block of $U$.

Observe that $X|{\psi }_{\text{good}{⟩}^{\otimes m}=\sin \left(\frac{\pi }{2k}\right)|\psi ⟩}$. Therefore, we aim to find a quantum circuit with unitary $U_{\Phi }$ such that $W{U}_{\Phi }V=\frac{1}{\sin \left(\frac{\pi }{2k}\right)}X$, implying $W{U}_{\Phi }V|{\psi }_{\text{good}}{⟩}^{\otimes m}=|0⟩$. By $X=WUV$, the absolute values of singular values of $X$ are $\sin \left(\frac{\pi }{2k}\right)$. Moreover, choose $P\left(x\right)=(-1{)}^k{T}_k(x)$, where $T_k$ is the Chebyshev polynomial of the first kind of order $k$. Then

implies that the QSVT of $X$ in terms of polynomial $P$ is a block encoding of $B:=\frac{1}{\sin \left(\frac{\pi }{2k}\right)}A$, as required.

We set $k=3$ so that $\sin \left(\frac{\pi }{2k}\right)=\frac{1}{2}$, and $U$ is a randomly chosen unitary. We want to show that the left-upper block of $U$ is amplified by 2 after QSVT.

As shown above, we successfully amplify $X$ by 2.

References¶

[1] Low, Guang Hao, and Isaac L. Chuang. "Hamiltonian simulation by qubitization." Quantum 3 (2019): 163.

[2] Gilyén, András, et al. "Quantum singular value transformation and beyond: exponential improvements for quantum matrix arithmetics." Proceedings of the 51st Annual ACM SIGACT Symposium on Theory of Computing. 2019.

[3] Camps, Daan, et al. "Explicit Quantum Circuits for Block Encodings of Certain Sparse Matrices." arXiv preprint arXiv:2203.10236 (2022).

[4] Clader, B. David, et al. "Quantum Resources Required to Block-Encode a Matrix of Classical Data." arXiv preprint arXiv:2206.03505 (2022).