Variational Quantum Metrology¶

Copyright (c) 2022 Institute for Quantum Computing, Baidu Inc. All Rights Reserved.

Background¶

Quantum metrology is the study of high resolution and high sensitivity measurements of physical parameters using quantum theory (e.g., quantum entanglement) in order to further describe physical systems. Its theoretical aspect is quantum parameter estimation theory, and its experimental aspect is called quantum sensing. Previous studies have shown that the estimation accuracy by quantum theory is improved by taking the square root of the required number of samples compared with the classical method [1-3]. For an unknown parameter, the goal of quantum metrology is to maximize the accuracy of parameter estimation while minimizing the required resources (such as time, number of qubits, etc.).

For example, given a unitary $e^{-i\varphi H}$ with a known Hamiltonian $H$, how can we extract the information about $\varphi$ by quantum metrology? It comprises the following four steps:

1. Preparation. Prepare an input state $|\psi ⟩$.
2. Parameterization. Obtain the parameterized quantum state $e^{-i\varphi H}|\psi ⟩$ after the evolution of $e^{-i\varphi H}$.
3. Measurement. Measure the output state.
4. Classical estimation. Estimate the parameters based on the results of multiple measurements.

Combined with quantum parameter estimation theory, this tutorial is based on the idea of variational quantum sensors in [4], and the parameterized quantum circuit is constructed using Paddle Quantum to train the loss function and obtain a quantum sensor that can estimate the parameters that are normally distributed.

Parameter Estimation Theory¶

Classical parameter estimation¶

Classical parameter estimation, such as the maximum-likelihood estimator (MLE), uses multiple samples to calculate data containing an unknown parameter. That is, given a probability distribution depending on an unknown parameter $\varphi$, where $f$ is the probability density function, and $X=\{X_1,X_2,...X_N\}$ is $N$ independent and identically distributed sample data, the estimated value $\hat{\varphi }$ is obtained by using MLE:

$$\begin{array}{}\hat{\varphi }\left(X\right)=\arg \underset{\varphi }{max}\prod _i^{N}f(X_i,\varphi ),& \text{(1)}\end{array}$$

which finds $\varphi$ such that $X_i(i=1,...,N)$ occurs with maximum probability. After obtaining the estimated parameters, how to measure the difference between the estimated parameters and the actual parameters? That is, how to measure the accuracy of the estimated parameters? In the parameter estimation theory, mean squared error (MSE) is generally used to measure the accuracy.

The sample containing the unknown parameter $\varphi$ is $X=\{X_1,X_2,...X_N\}\in F^N$, where $F^N$ is the sample space. Let $\hat{\varphi }\left(X\right):F^N\to \Phi$ be the estimator that estimates $\varphi \in \Phi$ ($\Phi$ is the parameter space). Then the MSE of $\hat{\varphi }\left(X\right)$ with respect to $\varphi$ is defined as

$$\begin{array}{}\begin{array}{cc}MSE& =E\left[\right(\hat{\varphi }\left(X\right)-\varphi {)}^2]\\ & =\sum _{X\in F^N}f(X;\varphi )\left(\hat{\varphi }\right(X)-\varphi {)}^2,\end{array}& \text{(2)}\end{array}$$

where $f(X;\varphi )$ is the probability density of getting the current sample $X$ given the parameter $\varphi$. Although different estimators affect the value of MSE, regardless of the choice of $\hat{\varphi }\left(X\right)$, there is $MSE\ge \frac{1}{NI\left(\varphi \right)}$. This lower bound is known as the Cramér–Rao (CR) bound [2], where $I\left(\varphi \right)$ is the Fisher information, which reflects to what extent a slight parameter change will change the probability distribution (see Quantum Fisher Information for the application of Fisher information in Paddle Quantum).

Quantum parameter estimation¶

In quantum parameter estimation, the samples used in classical parameter estimation become a quantum state ${\rho }_{\varphi }\in F\left(H\right)$ to be measured, where $\varphi$ is the unknown parameter and $F\left(H\right)$ denotes the set of density operators on the Hilbert space $H$. According to the steps of quantum metrology and [4], assuming that the initial input state is $|0⟩$ and the estimator is $\hat{\varphi }\left(m\right)$, where $m$ is related to the measured results (such as the difference in the number of 1s and the number of 0s in the measured bit string), then the MSE is

$$\begin{array}{}\begin{array}{cc}MSE& =E\left[\right(\hat{\varphi }\left(m\right)-\varphi {)}^2]\\ & =\sum _m\left(\hat{\varphi }\right(m)-\varphi {)}^{2}p(m|\varphi ),\end{array}& \text{(3)}\end{array}$$

where $p\left(m|\varphi \right)$ is the probability of obtaining $m$ by measurement with a given parameter $\varphi$. Similarly, no matter how $\hat{\varphi }\left(m\right)$ is chosen, there is a quantum CR bound $MSE\ge \frac{1}{NF\left(\varphi \right)}$, where $N$ is the number of repeated measurements of ${\rho }_{\varphi }$, and $F\left(\varphi \right)$ is the quantum Fisher information (see Quantum Fisher Information for the application of quantum Fisher information in Paddle Quantum).

Variational Quantum Sensors¶

Quantum sensing is the application of quantum metrology. Based on [4], this tutorial mainly introduces a kind of variational Ramsey interferometer. The traditional Ramsey interferometer [2] (as shown in Figure 1) is a particle interferometry method that uses magnetic resonance phenomena to measure particle transition frequency and is used to measure unknown parameters. The variational Ramsay interferometer [6] (as shown in Figure 2) consists of two parameterized quantum circuits (denoted as $U_{En}\left({\theta }_{En}\right)$ and $U_{De}\left({\theta }_{De}\right)$) in the encoding and decoding parts of the circuit for setting entanglement and measuring quantum states. Previous studies have shown that by combining with quantum theory (such as quantum entanglement), the scaling of parameter estimation accuracy is enhanced to $\frac{1}{N}$ from $\frac{1}{\sqrt{N}}$ [1-3], and the appropriate entanglement mode can be effectively found by the variational method.

Figure 1：Ramsey interferometer. On the left is the classical configuration of a Ramsey interferometer, and on the right is a Ramsey interferometer using quantum entanglement. Compared with the classical setting, the interferometer using quantum entanglement has an advantage in the order of square root in the accuracy of estimating unknown parameters.

Figure 2：Variational Ramsey interferometer. Two parameterized quantum circuits are optimized to find an efficient way of utilizing entanglement.

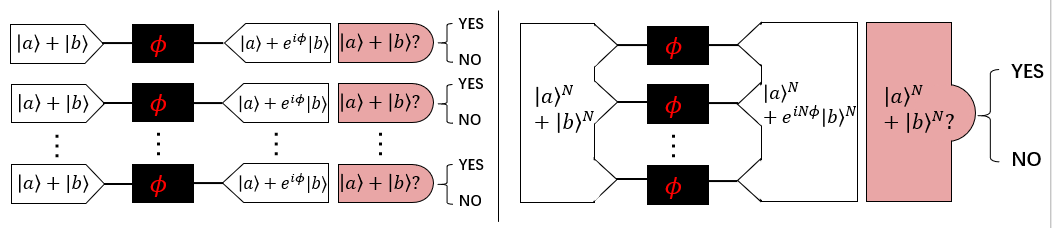
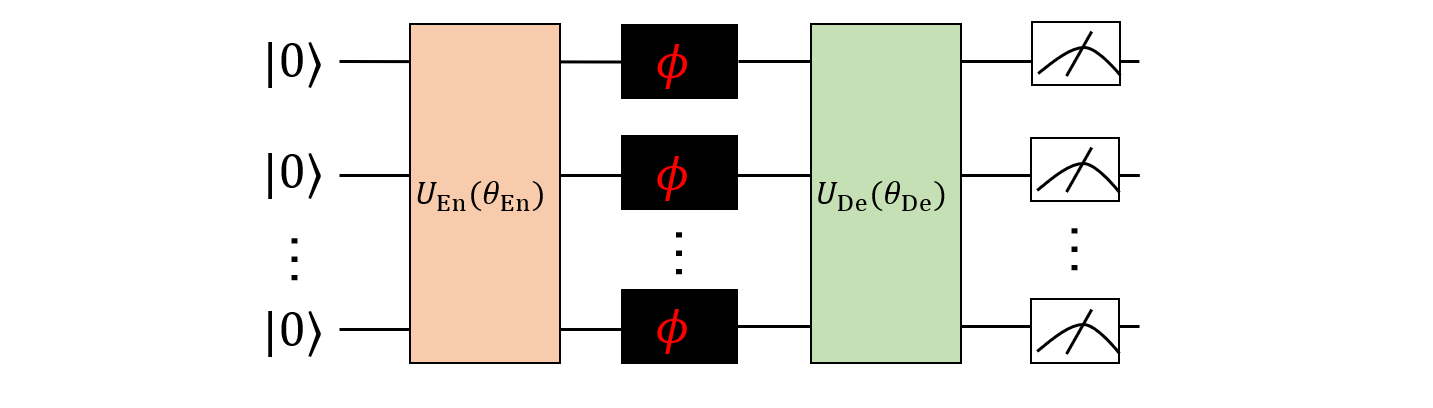
In the following, we construct a parameterized quantum circuit using Paddle Quantum to investigate the accuracy of estimating normally distributed parameters by a variational Ramsey interferometer. There are three steps as follows.

1. Initialization.
2. Evaluation.
3. Optimization.

The probability density function of the parameters that obey the normal distribution is:

$$\begin{array}{}f\left(x\right)=\frac{1}{\sqrt{2\pi }\nu }\exp (-\frac{(x-\mu {)}^2}{2{\nu }^2}),& \text{(4)}\end{array}$$

where $\mu$ is the mean and ${\nu }^2$ is the variance. In this case, the loss function of the variational Ramsey interferometer is:

$$\begin{array}{}C({\theta }_{En},{\theta }_{De},a)=\int d\varphi f\left(\varphi \right)MSE\left(\varphi \right),& \text{(5)}\end{array}$$

where the estimator is $\hat{\varphi }\left(m\right)=am$, $a$ is a parameter to be optimized, $m$ is the difference in the number of 1s and the number of 0s in the measured bit string, $MSE\left(\varphi \right)={\sum }_m\left(\hat{\varphi }\right(m)-\varphi {)}^2{p}_{\theta }(m|\varphi )$, and $\theta =({\theta }_{En},{\theta }_{De})$.

1. Initializaiton¶

• Set the input state as $|0⟩$.
• Construct the parameterized quantum circuits $U_{En}$ and $U_{De}$ for encoding and decoding, respectively.
• Encode the unknown parameter.

Let us import the necessary packages:

Next, we construct a parameterized quantum circuit of $N$ qubits to complete the initialization.

The whole circuit includes the following five parts.

• $R_y^{\otimes N}\left(\frac{\pi }{2}\right)$ gates.
• Encoding circuit $U_{En}\left({\theta }_{En}\right)$.
• Circuit with unknown parameter $R_z^{\otimes N}\left(\varphi \right)=e^{-i\varphi J_z}$, where $J_z=\frac{1}{2}{\sum }_{k=1}^N{\sigma }_z^{\left(k\right)}$.
• Decoding circuit $U_{De}\left({\theta }_{De}\right)$.
• $R_x^{\otimes N}\left(\frac{\pi }{2}\right)$ gate.

So the unitary of the entire circuit is

$$\begin{array}{}U(\varphi ,{\theta }_{En},{\theta }_{De})=R_x^{\otimes N}\left(\frac{\pi }{2}\right)U_{De}\left({\theta }_{De}\right)R_z^{\otimes N}\left(\varphi \right)U_{En}\left({\theta }_{En}\right)R_y^{\otimes N}\left(\frac{\pi }{2}\right).& \text{(6)}\end{array}$$

When the depth of the encoding circuit and decoding circuit is $0$, the entire circuit is the classical configuration of a Ramsey interferometer. Here we construct the encoding and the decoding circuits.

2. Evaluation¶

• Calculate the probability distribution of $m$.
• Calculate the MSE of the estimator $\hat{\varphi }\left(m\right)=am$: $MSE={\sum }_m\left(\hat{\varphi }\right(m)-\varphi {)}^2{p}_{\theta }(m|\varphi )$.
• Calculate the loss function. Here, we use the discrete form of the loss function to approximate its integral form:

$$\begin{array}{}C=\sum _{k=1}^t\frac{2}{t}f\left({\varphi }_k\right)MSE,& \text{(7)}\end{array}$$

where $t$ is the number of partitions in the selected interval (the total interval size is $2$ in this tutorial), and $f\left({\varphi }_k\right)$ is the probability corresponding to ${\varphi }_k$.

3. Optimization¶

The optimized circuit is used to estimate the parameters with a normal distribution, and then we draw the MSE.

Conclusion¶

We can see that the MSE estimated by the optimized quantum sensor is negatively correlated with the probability density of the parameters, and the value of MSE is the lowest near the mean value of the normal distribution, indicating that the obtained quantum sensor by variational method is effective for the parameters following a normal distribution.

---

References¶

[1] Braunstein S L, Caves C M. Statistical distance and the geometry of quantum states[J]. Physical Review Letters, 1994, 72(22): 3439.

[2] Giovannetti V, Lloyd S, Maccone L. Quantum metrology[J]. Physical review letters, 2006, 96(1): 010401.

[3] Tóth G, Apellaniz I. Quantum metrology from a quantum information science perspective[J]. Journal of Physics A: Mathematical and Theoretical, 2014, 47(42): 424006.

[4] Marciniak C D, Feldker T, Pogorelov I, et al. Optimal metrology with programmable quantum sensors[J]. Nature, 2022, 603(7902): 604-609.

[5] Giovannetti V, Lloyd S, Maccone L. Advances in quantum metrology[J]. Nature photonics, 2011, 5(4): 222-229.

[6] Kaubruegger R, Vasilyev D V, Schulte M, et al. Quantum variational optimization of Ramsey interferometry and atomic clocks[J]. Physical Review X, 2021, 11(4): 041045.